Взаимное расположение прямых в пространстве

Во-первых, две прямые могут совпадать, то есть, иметь бесконечно много общих точек (по крайней мере две общие точки).

Во-вторых, две прямые в пространстве могут пересекаться, то есть, иметь одну общую точку. В этом случае эти две прямые лежат в некоторой плоскости трехмерного пространства. Если две прямые в пространстве пересекаются, то мы приходим к понятию угла между пересекающимися прямыми.

В-третьих, две прямые в пространстве могут быть параллельными. В этом случае они лежат в одной плоскости и не имеют общих точек. Любой ненулевой вектор, лежащий на этой прямой или на прямой, которая параллельна данной, называется направляющим вектором прямой.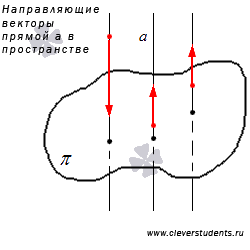

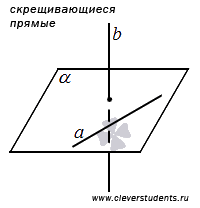
Наконец, две прямые в трехмерном пространстве могут быть скрещивающимися. Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости. Такое взаимное расположение двух прямых в пространстве приводит нас к понятию угла между скрещивающимися прямыми.

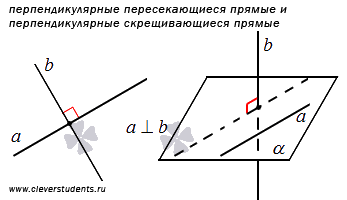
Когда угол между пересекающимися или скрещивающимися прямыми в трехмерном пространстве равен девяноста градусам - эти прямые называются перпендикулярными.

Date: 2015-08-15; view: 933; Нарушение авторских прав