Феноменологическая теория вращения плоскости поляризации

Как было отмечено, световая волна называется поляризованной по кругу (циркулярно поляризованной), если ее вектор напряженности электрического поля изменяется с течением времени так, что проекция траектории конца вектора на плоскость, перпендикулярную лучу, представляет собой окружность. Если электрический вектор при наблюдении навстречу световому лучу совершает вращение по часовой стрелке, циркуляцию принято называть правой; при вращении против часовой стрелки говорят о круговой поляризации по левому кругу.

Любая линейно поляризованная волна может рассматриваться как суперпозиция двух циркулярно поляризованных волн с правым и левым направлениями вращения электрического вектора, с одинаковыми частотами и амплитудами, распространяющихся в том же направлении, что и линейно поляризованная волна.

Впервые вращение плоскости поляризации было объяснено французским физиком О.Ж. Френелем (1817 г.), показавшим, что это явление сводится к особому типу двойного лучепреломления (круговому). Френель предположил, что при этом две монохроматические волны, которые могут распространяться в оптически активной среде с определенными, но различными фазовыми скоростями (υ _п ≠ υ _л) поляризованы не линейно, как при обычном (линейном) двойном лучепреломлении, а по кругу: одна по правому (υ _п), другая по левому (υ _л).

Гипотезу о возможности существования в активной среде этих циркулярно поляризованных волн, распространяющихся с различными скоростями, Френель теоретически доказать не мог, т.к. для этого необходимо было бы располагать полной системой уравнений волновой теории света в оптически активных средах. Но Френель подтвердил ее экспериментально, изготовив сложную призму (рис. 6.20), состоящую из трех призм: двух торцовых из правовращающего кварца (П) и средней с тупым преломляющим углом (~152°) из левовращающего кварца (Л). Оптические оси всех призм параллельны основанию. Если предположить, что в правовращающем кварце υ _п > υ _л (п _п < п _л), а в левовращающем – наоборот, то луч правой круговой поляризации при преломлении на внутренних гранях отклоняется в сторону основания средней призмы, а левой – в сторону вершины. Состояние круговой поляризации выходящих пучков (угол расхождения между которыми ~4°) непосредственно проверяется с помощью пластинки λ /4 и анализатора. Результаты эксперимента полностью подтвердили предположения Френеля.

Р и с. 6.20	Р и с. 6.21

Пусть на оптически активное вещество вдоль оси Oz падает линейно поляризованная волна (рис. 6.21):

.

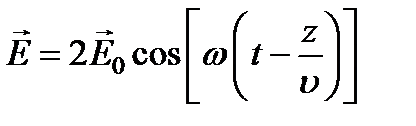Две циркулярно поляризованные волны (по левому и правому кругу), суперпозицией которых является падающая волна, для z = 0 в проекциях на оси Ox и Oy представляются:

, .

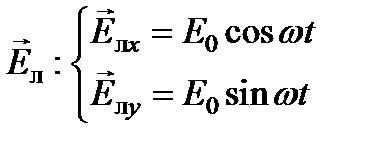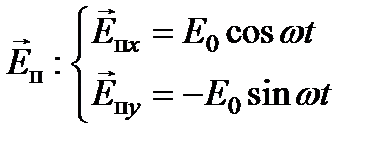Т.e. исходная линейно поляризованная волна в точке z = 0 имеет проекции вектора напряженности:

, .

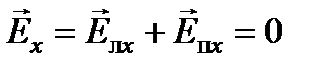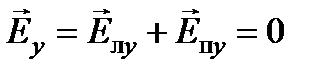В этом случае линия колебаний вектора (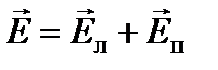) совпадает с осью Ox и образует равные углы с векторам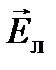и и 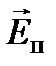. Если бы между колебаниями имелся сдвиг фаз, то линия колебаний суммарной напряженности образовала бы с осью Ox угол, определяемый сдвигом фаз слагаемых волн.

Обозначая скорости циркулярно поляризованных волн с векторам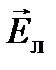и и 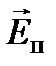, соответственно υ _л и υ _п, а коэффициенты преломления п _л и п _п, можно для выходящих из оптически активной среды циркулярно поляризованных волн записать: 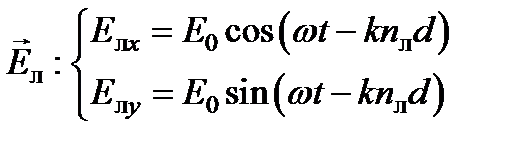, , 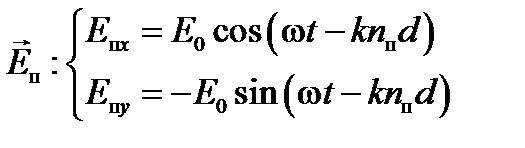где d – расстояние, пройденное волной во вращающей плоскость поляризации среде, k = 2 π / λ ₀ – волновое число, λ ₀ – длина волны в вакууме.

На выходе из оптически активной среды обе циркулярно поляризованные волны складываются снова в линейно поляризованную волну с плоскостью поляризации, относительно которой вектора 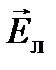и 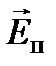будут расположены симметрично, занимающей, однако, иное положение, чем y = 0 (рис. 3). Найдем положение векторов 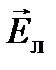и 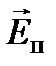в некоторый момент времени, например 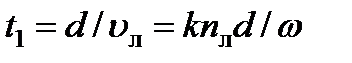. Тогда

, .

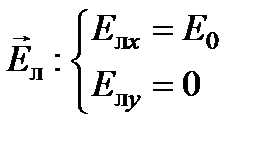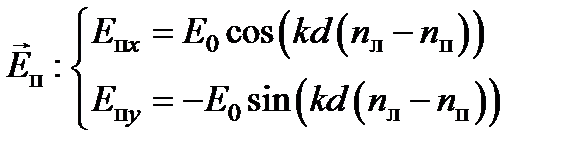Линия, относительно которой векторы 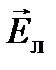и 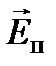расположены симметрично, является биссектрисой угла между этими векторами, обозначенного 2 φ и равного kd (n _л – n _п). Следовательно, плоскость поляризации после прохождения волной слоя активной среды толщиной d поворачивается на угол:

.

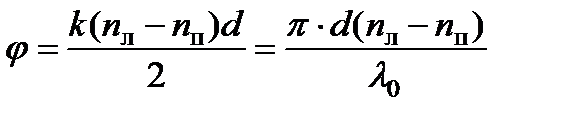Таким образом, получаем, что для правовращающих веществ υ _л < υ _п (n _л > n _п) (рассмотренный случай), а для левовращающих υ _л < υ _п (n _л < n _п), что и подтверждается описанным ранее экспериментом Френеля. Т.е. плоскость поляризации в активной среде вращается в ту же сторону, что и электрический вектор поляризованной по кругу волны с большей фазовой скоростью (с меньшим показателем преломления).

Р и с. 6.22

Сравнивая выражения и,, получаем для постоянной и удельной постоянной вращения:

, .

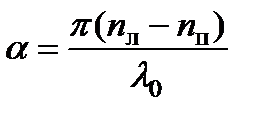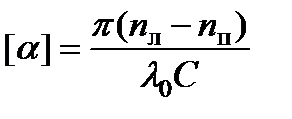Теория Френеля свела задачу о вращении плоскости поляризации к задаче объяснения кругового двойного лучепреломления, т.е. к более общей проблеме зависимости показателя преломления от характера поляризации света. Но причину различия в скоростях распространения лучей, поляризованных по правому и левому кругу, в оптически активных средах она не выяснила.

Date: 2015-08-06; view: 593; Нарушение авторских прав