Дифракционный интеграл Френеля

Рассмотрим элементарную теорию дифракции света, построенную по принципу Гюйгенса-Френеля.

Сначала запишем математическую формулировку принципа Гюйгенса-Френеля. Введём некоторую поверхность x, охватывающую источник света S, и будем считать каждый элемент ds этой поверхности источником вторичной сферической световой волны (рис. 4.2). Амплитуда вторичной световой волны, достигающей интересующей нас точки P, должна быть пропорциональной амплитуде первичной волны E_m, приходящей к элементу ds, а также площади самого элемента ds, и обратно пропорциональна расстоянию r от элемента ds до точки P.

Для определения результирующей амплитуды в точке P, т.е. суммы элементарных амплитуд, необходимо учесть, что колебания от разных элементов d s достигают точки P с разными фазами. Это приводит к появлению в выражении для результирующей амплитуды множителя cos(kr + a), где k = 2 p/l, а a – дополнительная фаза, равная фазе первичной волны на элементе ds, притом для разных элементов она в общем случае не одинакова.

Таким образом, результирующая амплитуда напряжённости E₀ (P) в точке P может быть представлена как суперпозиция элементарных амплитуд с учётом их взаимных фазовых соотношений:

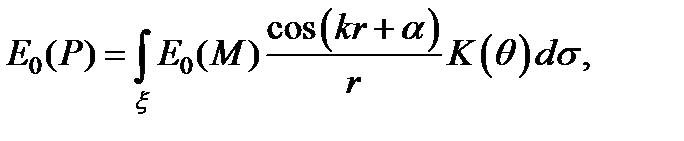
где интегрирование проводится по всей поверхности, окружающей источник.

В интеграле K (q) – некоторый “коэффициент наклона”, учитывающий то обстоятельство, что вклад элемента ds в результирующее поле зависит от ориентации данного элемента поверхности по отношению к направлению на точку наблюдения.

Формулу можно записать через показательную функцию в виде:

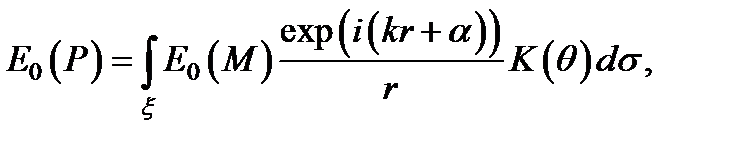
где E ₀(P) и E ₀(M) – в общем случае комплексные амплитуды поля в точке P и в точке M соответственно.

Интеграл носит название интеграла Гюйгенса-Френеля. Формула построена на основе качественных физических соображений. Наиболее существенно то, что интеграл Гюйгенса-Френеля учитывает фазы элементарных вторичных волн, приходящих в точку P от различных элементов поверхности x, т.е. принимается во внимание интерференция вторичных волн.

Функция K (q) в остаётся пока неопределённой. Френель полагал, что K (q) монотонно убывает от некоторого начального значения K (0) до нуля при изменении q от нуля до p /2. Как мы увидим дальше, многие практически важные задачи можно решить, не уточняя конкретного вида зависимости его от угла q.

В дальнейшем будем рассматривать ситуации, позволяющие в качестве поверхности x брать волновую поверхность падающей волны, что значительно упрощает расчёты, например, в формуле дополнительную фазу a можно считать равной нулю, a = 0.

Зоны Френеля. Суммирование (интегрирование) амплитуд элементарных колебаний, приходящих в точку P, вообще говоря, весьма сложно. Но в простейших случаях, обладающих определённой симметрией, интегрирование, как показал Френель, может быть заменено простым алгебраическим или графическим сложением (последнее особенно наглядно).

Приближённый способ расчёта дифракционных картин основан на представлении о так называемых полуволновых зонах или зонах Френеля, на которые разбивается поверхность x, и конфигурация которых зависит от симметрии рассматриваемой задачи.

Если, например, источник S точечный, и волна изотропная, то удобно вспомогательную поверхность x выбрать в виде сферы радиуса a с центром в точке S (рис. 4.3).

Согласно принципу Гюйгенса-Френеля, данную поверхность можно рассматривать как источник вторичных световых волн с одинаковой начальной фазой. Выделим на сфере кольцевые зоны так, чтобы расстояния от границ зоны до точки наблюдения отличались на половину длины световой волны. Для этого из точки Р мысленно проводим сферы радиусами b, b + 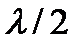, b +2 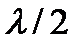, … b + m .

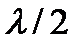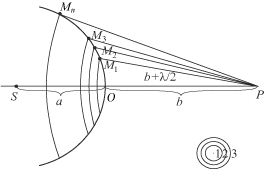
Р и с. 4.3

Обозначая границы зон буквами M ₁, M ₂, M ₃, …, получим:

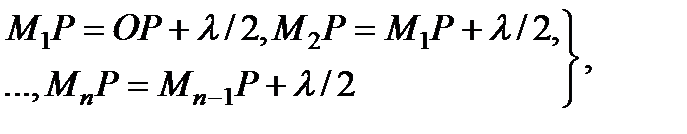
где l – длина световой волны, P – точка наблюдения, O – центр первой зоны (рис. 4.3). Заметим, что положение границ френелевских зон зависит от выбора точки наблюдения. Смысл разбиения поверхности x на зоны состоит в том, что разность фаз элементарных вторичных волн, приходящих в точку наблюдения от данной зоны, не превышает величины p. Сложение таких волн приводит к их взаимному усилению. Поэтому каждую зону Френеля можно рассматривать как источник вторичных волн, имеющих определённую фазу. Напротив, две соседние зоны Френеля действуют как источники, колеблющиеся в противофазе.

Размеры зон Френеля. Для того, чтобы оценить относительный вклад френелевских зон в интеграл, оценим радиусы зон и их площади.

На рис. 4.4 показаны точечный источник света S, точка наблюдения поля P, часть сферической поверхности x (источника вторичных волн) и внешняя граница первой зоны Френеля. Пусть a – радиус сферы, b – кратчайшее расстояние от точки P до сферы, r – радиус первой световой зоны Френеля. Из рис. 4.4 видно, что: 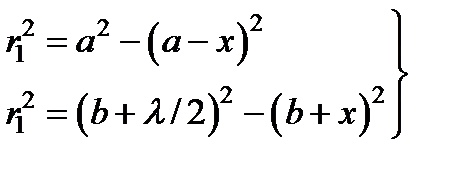откуда запишем: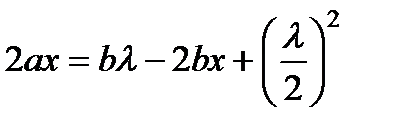

Р и с. 4.4

Как правило, в оптике справедливо приближение: ,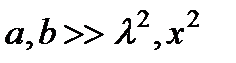

поэтому пренебрегая слагаемыми, которые пропорциональны l ² и x ², получим из и:

, ,

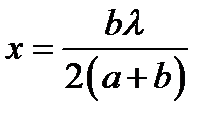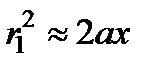откуда: 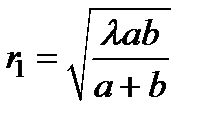. Аналогичным образом находим внешний радиус m -й зоны Френеля:

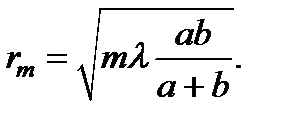Площади зон (при достаточно малых m): 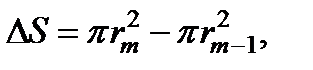или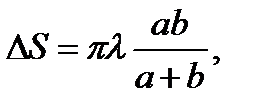

т.е. практически одинаковы. Но амплитуды колебаний, приходящих в точку P от зон, монотонно и слабо убывают из-за увеличения расстояния r до точки P от каждой следующей зоны и роста угла q между нормалью к элементам зоны и направлением на точку P.

Физическое содержание задачи почти не измениться, а формулы станут проще, если вместо сферической волны точечного источника рассмотреть плоскую световую волну. В данном случае зоны Френеля представляют собой кольца на плоскости. Их радиусы и площади можно подсчитать по формулам и, полагая a ® ¥. Получим: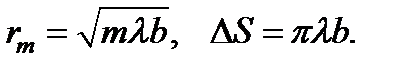

Date: 2015-08-06; view: 1441; Нарушение авторских прав