
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Дифракция Френеля на простейших препятствиях. Графический способ решения дифракционных задач. Спираль Френеля
|
|
Вычисление результирующего светового поля, описываемого интегралом Гюйгенса-Френеля, сводится к суммированию световых колебаний, возбуждаемых элементарными вторичными источниками. С математической точки зрения задача сводиться к суммированию гармонических колебаний, имеющих одну и ту же частоту, но разные амплитуды и фазы. Наглядный способ решения этой задачи – построение векторной диаграммы. Как известно, гармонические колебания с амплитудой a и фазой j можно охарактеризовать комплексной амплитудой E = a exp(ij) либо вектором на плоскости переменных Re E и Im E, причём длина вектора равна a, а угол наклона к оси Re E равен j. Сумма нескольких гармонических колебаний частоты w с произвольными амплитудами и фазами есть также гармоническое колебание на частоте w. Действительную амплитуду и фазу результирующего колебания можно найти, откладывая по правилу сложения векторов векторы, изображающие колебания-слагаемые. После построения векторной суммы, амплитуда результирующего колебания находится как длина полученного вектора-суммы, а фаза результирующего колебания – как угол наклона этого вектора к оси абсцисс.
Спираль Френеля. Применим описанный метод для расчёта дифракционного интеграла Гюйгенса-Френеля. Сначала вычислим вклад в дифракционный интеграл, например, первой зоны Френеля. Для этого разбиваем зону Френеля на множество подзон. Разбиение производим таким образом, чтобы площади подзон были примерно одинаковы, а число подзон было достаточно большим. В этом случае вклады подзон можно изобразить векторами, которые имеют почти одинаковую длину, но разные углы наклона к оси абсцисс. Первый и последний векторы будут повёрнуты друг относительно друга на угол p – в соответствии с определением зоны Френеля. По мере увеличения радиуса вклад подзоны (и, следовательно, длина соответствующего вектора) немного уменьшается вследствие увеличения угла между нормалью к поверхности и направлением на точку наблюдения (рис. 4.5 а).
| г) |
| в) |
| б) |
| а) |
 Р и с. 4.5
Р и с. 4.5
Аналогичным образом строится вектор, изображающий вклад в дифракционный интеграл второй зоны Френеля (рис. 4.5 б), а также первый и второй зон вместе (рис. 4.5 в). С увеличением номера зоны, элементарные векторы, изображающие действие её подзон, становятся короче. Это отражает уменьшение общего вклада данной зоны в суммарное дифракционное поле (E 2 < E 1), связанное с увеличением угла наклона зоны, т.е. с фактором K (q) и увеличение расстояния r (для сферической волны).
Продолжая процедуру построения векторной диаграммы для всё большего числа зон, получаем скручивающуюся спираль. При увеличении числа подзон каждой зоны, ломанная линия векторной диаграммы всё больше приближается к гладкой кривой. В предельном случае, когда открыты все зоны Френеля, и число подзон в каждой зоне стремиться к бесконечности, получим векторную диаграмму, показанную на рис. 4.5 г. Эта предельная диаграмма имеет вид гладкой скручивающейся спирали – спирали Френеля. Рассмотрим несколько примеров.
Дифракция на круглом отверстии. Пользуясь методом Френеля, определим амплитуду световых колебаний в точке P за круглым отверстием на его оси (рис. 4.6). Волновая поверхность, которой мы перекроем отверстие, симметрична относительно прямой SP, поэтому её наиболее целесообразно разбивать на кольцевые зоны с центром на оси отверстия.

Р и с 4.6

Поскольку фазы колебаний, возбуждаемых в точке P соседними зонами, отличаются на p, поэтому результирующая амплитуда, а значит и интенсивность, зависит от того, чёткое или нечёткое число m зон Френеля умещается в отверстии – для данной точки наблюдения P. Если число зон нечётное, в точке P наблюдается максимум, если же число чётное, то – минимум. Чтобы найти число зон, открываемых отверстием, воспользуемся рис. 4.7.
Р и с. 4.7
Если радиус отверстия r совпадает с внешним радиусом m -ой зоны (rm = r), то отрезок CO равен:

Выразим ha и hb через r и соответствующие радиусы сфер, проведенных из точек S и P (SO = a и CP = b + ml /2). Согласно теореме Пифагора: 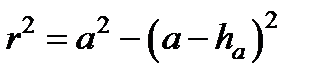 .
.
Пренебрегая ha 2 (обычно ha << 2 a), предыдущее равенство можно записать так: 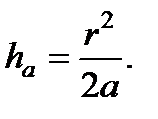
Рассуждая аналогично для правой части рис. 4.7, получим следующее выражение:
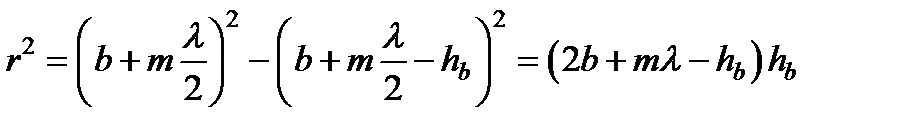 .
.
Пренебрегая в последней скобке слагаемыми ml и hb по сравнению 2 b, приходим к выводу, что
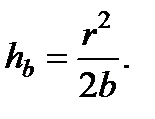
Остаётся подставить и в исходную формулу и получим, что: 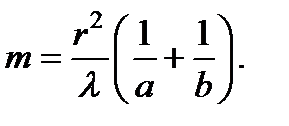
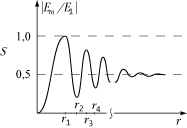
По мере увеличения радиуса отверстия амплитуда колебаний и интенсивность света в точке P (рис. 4.5) изменяется не монотонно. Пока открывается первая зона Френеля, амплитуда увеличивается и достигает максимума при полностью открытой зоне (рис. 4.5 а). Но по мере открывания второй зоны Френеля амплитуда колебаний убывает, и при полностью открытых двух первых зонах уменьшается почти до нуля (рис. 4.5 б). Затем амплитуда увеличивается снова и так далее (рис. 4.8).
На рис. 4.8 r 1, r 2, … – радиусы френелевских зон. То же самое будет наблюдаться, если вместо увеличения радиуса отверстия приближать к нему точку наблюдения P вдоль линии SP (рис. 4.6). При этом число открываемых зон в отверстии будет увеличиваться, что лёгко понять из данного рисунка, а также следует из формулы.
Как видно из рис. 4.5 г, амплитуда колебаний от полностью открытой волновой поверхности равна E ¥ = E 1/2, т.е. интенсивность (I ~ E 2) в четыре раза меньше, чем при наличии экрана с круглым отверстием, открывающем только первую зону Френеля.
Особенно неожиданным в методе Френеля представляется вывод, что при отверстии в экране, открывающем для точки P две зоны Френеля, интенсивность в этой точке падает практически до нуля, хотя световой поток через отверстие увеличивается вдвое.
Результаты, предсказанные на основе принципа Гюйгенса-Френеля, выглядят на первый взгляд парадоксально, но они хорошо подтверждаются опытом. Эти результаты противоречат законам геометрической оптики, согласно которым интенсивность в точке P не должна зависеть от радиуса отверстия.
Р и с. 4.8 Р и с. 4.9
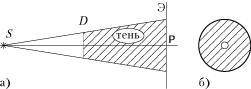
Дифракция на диске. Пятно Пуассона. Предположим, что световая волна падает на круглый непрозрачный диск D радиуса r, а наблюдение ведётся в некоторой точке P, расположенной в области геометрической тени на оси диска (рис. 4.9 а).
Оказалось, что за круглым непрозрачным диском в центре его геометрической тени интенсивность не равна нулю (рис. 4.9 б). Если диск перекрывает лишь несколько зон, то интенсивность в центре тени почти такая же, как при отсутствии диска. Это непосредственно следует из спирали Френеля (рис. 4.10), поскольку если диск закрывает, скажем, 1,5 зоны Френеля, то результирующий вектор 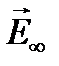 при полностью открытой волновой поверхности можно представить как сумму двух векторов:
при полностью открытой волновой поверхности можно представить как сумму двух векторов: 
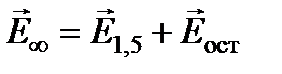 .
.
Так как первые полторы зоны закрыты, то остаётся только вектор 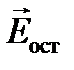 – от всех остальных зон.
– от всех остальных зон.
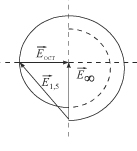
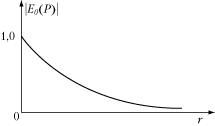
Р и с. 4.10 Р и с. 4.11
Этот вектор по модулю лишь немного меньше вектора 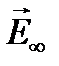 . Светлое пятно в центре геометрической тени называют пятном Пуассона. Рассматривая в своё время метод Френеля, Пуассон пришёл к выводу, что в центре тени от диска должно быть светлое пятно, но счёл этот вывод столь абсурдным, что выдвинул его как убедительное возражение против волновой теории, развиваемой Френелем. Однако это “абсурдное” предсказание было экспериментально подтверждено в опытах Араго, что свидетельствовало в пользу волновой теории света.
. Светлое пятно в центре геометрической тени называют пятном Пуассона. Рассматривая в своё время метод Френеля, Пуассон пришёл к выводу, что в центре тени от диска должно быть светлое пятно, но счёл этот вывод столь абсурдным, что выдвинул его как убедительное возражение против волновой теории, развиваемой Френелем. Однако это “абсурдное” предсказание было экспериментально подтверждено в опытах Араго, что свидетельствовало в пользу волновой теории света.
По мере увеличения радиуса диска r амплитуда колебаний в точке P монотонно уменьшается (рис.4.11), но даже в случае достаточно большого экрана, закрывающего сразу несколько зон Френеля, интенсивность света в центре геометрической тени отлична от нуля.
Построение векторов амплитуды поля с помощью спирали Френеля, подтверждающее монотонное убывание амплитуды колебаний, представлено на рис. 4.12 для случаев, когда r = 0 (а), r = r 1 (б), r = r 2 (в), r = r 3 (г).
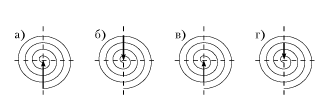
Р и с. 4.12
Зонная пластинка. Если в экране открыть только нечетные зоны Френеля (1-ю, 3-ю,...), то векторы-амплитуды от этих зон будут сонаправлены и в сумме дадут вектор, во много раз превосходящий по модулю векторы E ¥ и E 1. Такой экран называют зонной пластинкой. Аналогично можно изготовить зонную пластинку, где открыты только четные зоны Френеля.
Зонная пластинка, содержащая n открытых зон, создает в точке Р интенсивность приблизительно в п 2 раз большую, чем отверстие в первую зону Френеля.
Усиление интенсивности света зонной пластинкой эквивалентно фокусирующему действию линзы. Расстояния от зонной пластинки до источника S и его «изображения» Р связаны таким же соотношением, как и соответствующие расстояния для линзы. Чтобы в этом убедиться, достаточно переписать формулу в виде 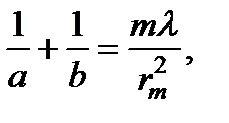 где выражение в правой части равенства можно рассматривать как 1/ f,
где выражение в правой части равенства можно рассматривать как 1/ f,
f – фокусное расстояние: f = 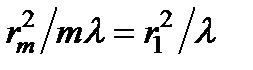 , поскольку
, поскольку 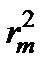 ~ m. Но в отличие от линзы, зонная пластинка – система не таутохронная: колебания, приходящие в фокус F от соседних открытых зон, различаются по фазе на 2 p (разность хода l). Кроме этого фокуса (основного), зонная пластинка имеет и другие, а именно те точки ', в которые колебания от соседних открытых зон приходят с разностью хода 2 l, 3 l, и т.д. Эти фокусы оказываются более слабыми по сравнению с основным.
~ m. Но в отличие от линзы, зонная пластинка – система не таутохронная: колебания, приходящие в фокус F от соседних открытых зон, различаются по фазе на 2 p (разность хода l). Кроме этого фокуса (основного), зонная пластинка имеет и другие, а именно те точки ', в которые колебания от соседних открытых зон приходят с разностью хода 2 l, 3 l, и т.д. Эти фокусы оказываются более слабыми по сравнению с основным.
Интенсивность света в главном фокусе зонной пластинки можно увеличить еще в четыре раза, если изменить на p фазы вторичных волн, исходящих из всех зон Френеля с четными (или нечетными) номерами. Тогда векторы-амплитуды от всех зон будут сонаправлены и результирующая амплитуда возрастет еще вдвое. Такая пластинка была изготовлена Вудом путем травления в соответствующих зонах тонкого лакового покрытия. Ее действие вполне эквивалентно действию линзы, так как в обоих случаях вторичные волны от всех точек волновой поверхности приходят в точку фокуса в одинаковых фазах.
Date: 2015-08-06; view: 1072; Нарушение авторских прав