Многолучевая интерференция. При падении пучка света на прозрачную пластинку на ее поверхности происходят многократные отражения

При падении пучка света на прозрачную пластинку на ее поверхности происходят многократные отражения, в результате чего с каждой стороны пластинки выходит ряд пучков с убывающей амплитудой. Рассматривая интерференционные эффекты, возникающие с такими, мы пренебрегали вкладом в результирующую интенсивность пучков, испытавших больше двух отражений. Такое допущение оправдано при малой отражательной способности поверхностей. Теперь мы учтем все отраженные пучки и покажем, что при большой отражательной способности поверхностей распределение интенсивности в интерференционной картине изменяется.

Рассмотрим плоскопараллельную прозрачную пластинку с показателем преломления n ₂, находящуюся в среде с показателем преломления n ₁, и предположим, что на эту пластинку под углом j ₁ падает плоская волна монохроматического света. Пусть луч CB ₁ (рис. 3.20) представляет направление распространения падающей волны.

Р и с. 3.20

На первой поверхности эта волна разделяется на две плоские волны: одну, отраженную в направлении B ₁ C ₁ и другую, прошедшую в пластинку в направлении B ₁ D ₁. Прошедшая волна падает на вторую поверхность под углом j ₂ и здесь снова разделяется на две плоские волны: одну, прошедшую в направлении D ₁ E ₁, и другую, отраженную обратно в пластинку в направлении D ₁ B ₂. Такой процесс деления волны, остающейся в пластинке, продолжается как показано на рисунке.

Пусть E ₀ - амплитуда электрического вектора падающей волны. E ₀ может быть комплексной. Она содержит постоянную часть фазы соответствующей волновой функции. Переменная часть ее, как известно, имеет вид (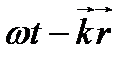). Для каждого члена совокупности отраженных или прошедших волн переменная часть фазы волновой функции отличается от такой же части фазы предыдущего члена на величину, соответствующую двукратному прохождению луча в пластинке. Эта разность фаз равна

,

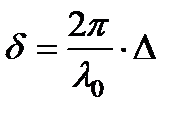где l ₀ - длина волны в вакууме, D - оптическая разность хода для любой пары соседних лучей. Например, для лучей B ₁ C ₁ и B ₂ C ₂, как видно из рис. 3.20,

,

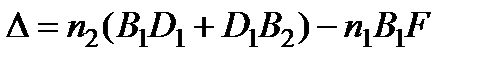где F - основание перпендикуляра, опущенного из B ₂ на B ₁ C ₁. Если h - толщина пластинки, а j ₁ и j ₂ — углы падения и преломления на верхней поверхности, то Согласно ,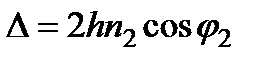

а соответствующая разность фаз, равна .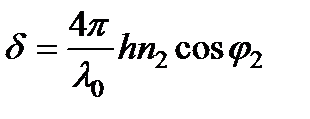

Следует также учитывать изменение фазы на p, которое, согласно формулам Френеля, происходит при каждом отражении от верхней или нижней поверхности. Полная разность фаз равна поэтому

.

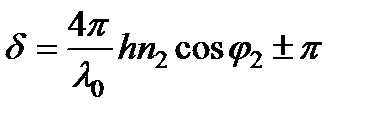Если взять любую пару прошедших через пластинку лучей (например, D ₁ E ₁ и D ₂ E ₂), то для них полная разность фаз определяется формулой. Луч D ₂ E ₂ дважды испытывает отражение (т.т. D ₁ и B ₂) в одинаковых условиях. Изменение фазы за счет отражения будет равно или 0 (если n ₂ > n ₁), или 2 p (если n ₁ > n ₂) и оно не учитывается.

Пусть для волны, идущей из окружающей среды в пластинку, r –коэффициент отражения (отношение амплитуд отраженной и падающей волны), а t – коэффициент пропускания (отношение амплитуд прошедшей и падающей волны); пусть далее r ¢ и t ¢ – соответствующие коэффициенты для волны, идущей из пластинки в окружающую среду. Вообще говоря, эти коэффициенты зависят от угла падения и состояния поляризация света, для границы двух прозрачных сред это показано с помощью формул Френеля. Если мы ограничимся малыми углами j ₁, то t и r практически не зависят от угла падения и от поляризации падающего света и для них можно принять значения, соответствующие нормальному падению, а именно:

.

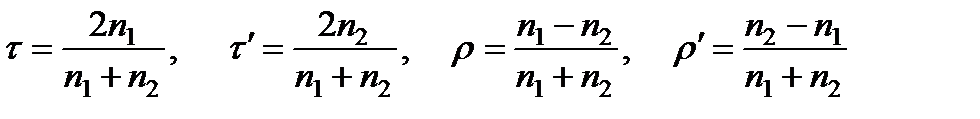На границе прозрачных сред t и r вещественны, а отрицательное значение r при n ₂ > n ₁ учитывает изменение фазы волны на p при отражении от оптически более плотной среды. Из формул легко видеть, что отражательная способность границы, или энергетический коэффициент отражения R, не зависит от того, идет свет из окружающей среды в пластинку или наоборот

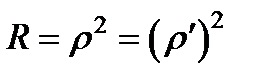, и что .

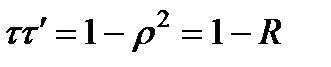Поэтому комплексная амплитуда всей прошедшей волны представится геометрической прогрессией:

.

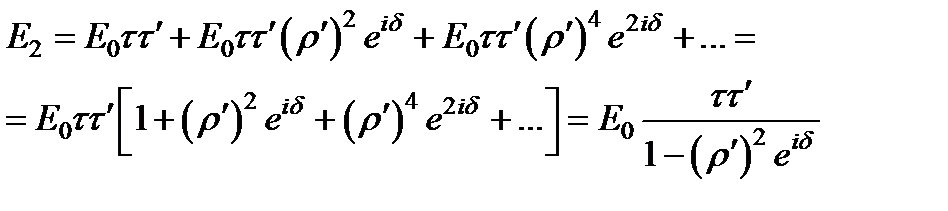Мы считаем, что пластинка достаточно длинная, так что число прошедших и отраженных лучей велико. Для нахождения интенсивности прошедшей волны умножим E ₂ в на комплексно-сопряженную величину и воспользуемся формулами и: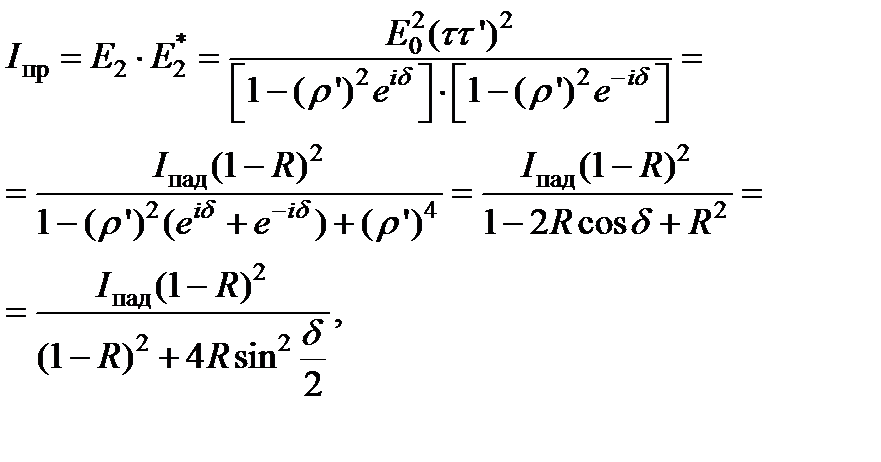

где .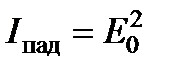

Таким же способом легко получить выражение для амплитуды отраженной волны:

.

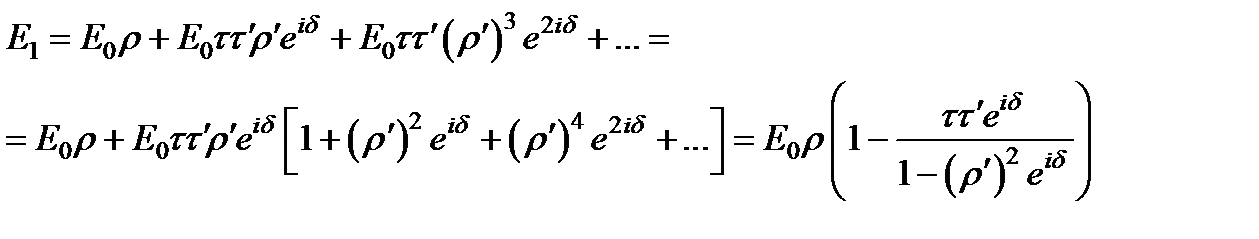Здесь учтено, что r ¢=- r. Для интенсивности отраженной волны находим

.

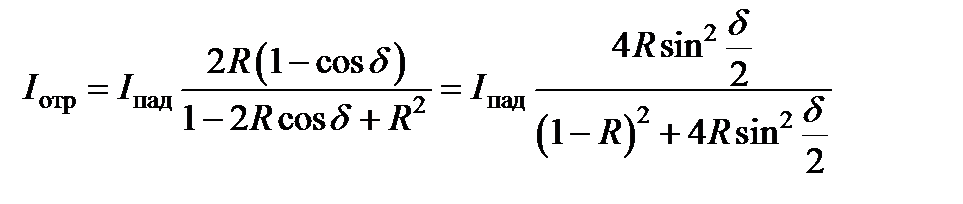Соотношения и известны как формулы Эйри. Из них видно, что I _пр + I _отр = I _пад, как и должно быть при отсутствии поглощения.

Предположим теперь, что плоские волны равной интенсивности падают на пластинку под разными, мало различающимися углами и прошедший свет собирается линзой L. В некоторой точке P ее фокальной плоскости интенсивность прошедшего света относится к интенсивности в отсутствие пластинки, как I _пр / I _пад. Следовательно, формула дает распределение интенсивности в многолучевой интерференционной картине, наблюдаемой в фокальной плоскости линзы, там, где при отсутствии пластинки была бы равномерная освещенность. Максимумы I _пр / I _пад = 1 получаются при d /2 = mp (m – целое число). Подставляя сюда d из, получаем то же условие, что и при двухлучевой интерференции, а именно ,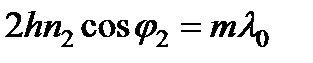

соответственно для минимума .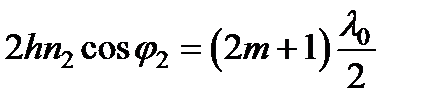

При малом коэффициенте отражения R < < 1 формулы и дают то же самое распределение интенсивности, что и при двухлучевой интерференции. Это распределение, однако, существенно изменяется при увеличении R, в особенности, когда R приближается к единице. На рис. 3.21, а приведены построенные по формуле кривые интенсивности прошедшего света в зависимости от d.

При R < < 1 они имеют вид, типичный для двух интерферирующих пучков. С увеличением коэффициента отражения максимумы сужаются, а в промежутках между ними интенсивность становится очень мала. Отношение интенсивности в максимумах и минимумах, характеризующее контрастность интерференционных полос, как видно из, определяется только коэффициентом отражения:

.

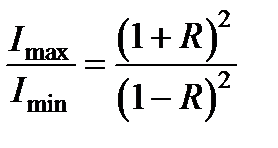Многолучевая интерференционная картина в прошедшем свете при значениях R, близких к единице, имеет вид узких светлых полос на почти совершенно темном фоне.

Подобное пространственное перераспределение поток энергии с концентрацией его в некоторых преимущественных направлениях всегда возникает при интерференции многих пучков. Чтобы наблюдались полосы, плоскопараллельную однородную пластинку нужно освещать рассеянным пучком, в котором имеются лучи самых разных направлений. Каждая интерференционная полоса образована лучами, падающими на пластинку под одинаковыми углами. Такие полосы носят название полос равного наклона. Так как каждая точка интерференционной полосы образована лучами, которые до прохождения линзы образуют параллельный пучок, то полосы локализованы в бесконечности (или в фокальной плоскости линзы). Полосы равного наклона имеют вид концентрических колец с центром на оси линзы. Центру картины соответствует наибольший порядок интерференции.

Р и с. 3.21

Аналогично, если свет, отраженный от пластинки, собирается линзой L ¢, то в ее фокальной плоскости так же появляются линии равного наклона. Из сравнения формул и следует, что I _отр + I _пр = I _пад, поэтому в отраженном свете наблюдается дополнительная картина, т.е. там, где в отраженном свете наблюдается максимум, в проходящем будет минимум и наоборот. Это связано с тем, что разность фаз лучей в отраженном и проходящем свете, согласно и, различается на p. Кроме того, различным будет и качество картин. Полосы имеют вид узких темных колец на почти равномерном светлом фоне (рис. 3.21, б). Резкость полос принято измерять полушириной интенсивности или просто полушириной максимума.

Для картины в прошедшем свете она равна расстоянию между точками, лежащими по обе стороны максимума в том месте, где интенсивность уменьшается до половины максимальной величины. Отношение расстояния между соседними полосами к полуширине называют резкостью полос и обозначают буквой F. У полосы целого порядка m точки, где интенсивность равна половине максимальной величины находятся при

,

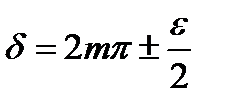где e в соответствии с определяется соотношением

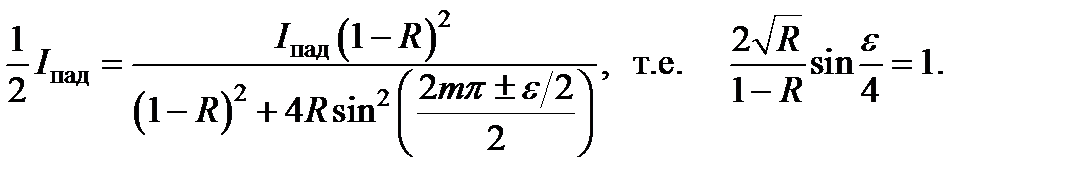
Когда R достаточно велико, то e настолько мало, что в последнем соотношении мы сможем принять sin (e /4) @ e /4, и получим для полуширины .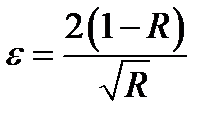

Так как расстояние между соседними полосами соответствует изменению d на 2 p, то для резкости находим .

До сих пор мы предполагали, что свет строго монохроматичен. В случае немонохроматического света распределение интенсивности равно сумме распределений интенсивностей типа, обусловленных каждой монохроматической компонентой. Из предыдущего ясно, что положение максимумов и минимумов зависит от длины волны монохроматической компоненты. Кроме того, при увеличении R распределение интенсивности становится более благоприятным для определения положения максимума, т.е. полосы, принадлежащие различным монохроматическим компонентам, в интерференционной картине в проходящем свете разделяются более четко. По этим причинам многолучевая интерференция находит большое практическое применение.