Интерференционная картина, получаемая с помощью плоскопараллельной пластинки

Рассмотрим сначала идеализированный случай, когда плоскопараллельная пластинка из прозрачного изотропного материала освещается точечным источником монохроматического света.

Р и с. 3.15 Р и с. 3.16

От точечного источника S в любую точку P могут попадать, вообще говоря, только два луча - один, отразившийся от верхней поверхности пластинки, и другой, отразившийся от нижней ее поверхности (рис. 3.15). Отсюда следует, что в случае точечного монохроматического источника света каждая точка пространства характеризуется вполне определенной разностью хода приходящих в нее отраженных лучей. Эти лучи, интерферируя, образуют устойчивую во времени интерференционную картину, которая должна наблюдаться в любой области пространства. Про соответствующие полосы интерференции говорят, что они не локализованы (или локализованы всюду).

При увеличении размеров источника в направлении, параллельном плоскости SNP, интерференционные полосы становятся менее четкими. Важным исключением является случай, когда точка P находится в бесконечности, а наблюдение интерференционной картины ведется либо глазом, аккомодированным на бесконечность, либо в фокальной плоскости объектива (рис. 3.16). В этих условиях оба луча, идущих от S к P, а именно лучи SANP и SABCEP, происходят от одного падающего луча, и после прохождения пластинки параллельны. Оптическая разность хода между ними равна:

,

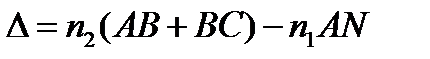где n ₂ и n ₁ - показатели преломления пластинки и окружающей среды,

N - основание перпендикуляра, опущенного из С. Фокальная плоскость объектива и параллельная ей плоскость NC являются сопряженными, и линза не вносит между лучами дополнительной разности хода.

Если h - толщина пластины, а j ₁ и j ₂ - углы падения и преломления на верхней поверхности, то

,

.

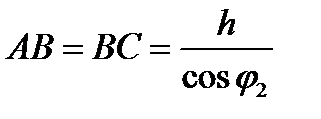Из предыдущих формул, с учетом закона преломления

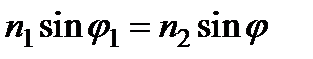
получаем, что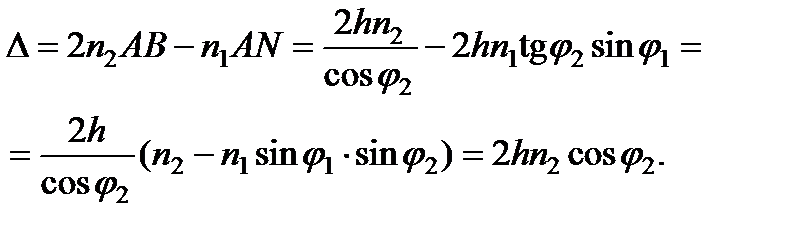

Соответствующая разность фаз равна: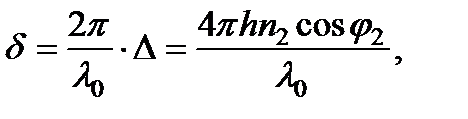

где l ₀ - длина волны в вакууме.

Следует также учитывать изменение фазы на p, которое, согласно формулам Френеля, происходит при каждом отражении от более плотной среды (мы рассматриваем только электрическую компоненту поля волны). Поэтому полная разность фаз в точке P равна:

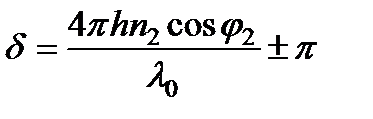или .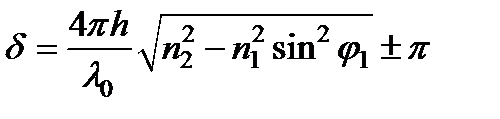

Угол j ₁, от значения которого зависит разность фаз, определяется только положением точки P в фокальной плоскости объектива, следовательно, разность фаз d не зависит от положения источника S. Отсюда вытекает, что при использовании протяженного источника полосы оказываются столь же отчетливыми, как и с точечным источником. Но так как это справедливо только для определенной плоскости наблюдения, то про такие полосы говорят, что они локализованы, и в данном случае - локализованы в бесконечности (или в фокальной плоскости объектива).

Если интенсивности рассматриваемых когерентных лучей обозначить соответственно I ₁ и I ₂, то полная интенсивность I в точке P определится соотношением:

,

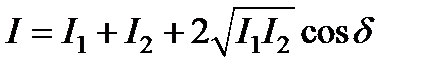откуда находим, что светлые полосы расположены при d = 2 mp или

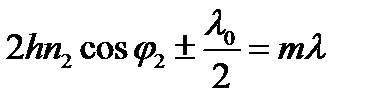, m = 0, 1, 2,...,

а темные полосы - при d = (2 m + 1) p или

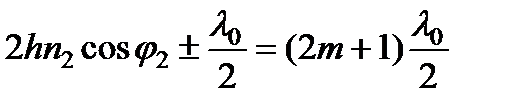, m = 0, 1, 2,.

Заданная интерференционная полоса характеризуется постоянством величины j ₂ (а значит и j ₁ ) и, следовательно, создается светом, падающим на пластинку под каким-то определенным углом. Поэтому такие полосы часто называют полосами равного наклона.

Если ось объектива нормальна к пластине, то при отражении света, близком к нормальному, полосы имеют вид концентрических колец с центром в фокусе. Порядок интерференции максимален в центре картины, где его величина m ₀ определяется соотношением: .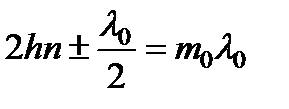

Мы рассматриваем пока только свет, отраженный от пластинки, но подобные рассуждения применимы и для света, прошедшего сквозь пластинку. В этом случае (рис. 3.17) в точку P фокальной плоскости объектива приходят от источника S два луча: один, прошедший без отражений, и другой - после двух внутренних отражений.

Р и с. 3.17

Оптическую разность хода этих лучей находят таким же образом, как и при выводе формулы, т.е.

,

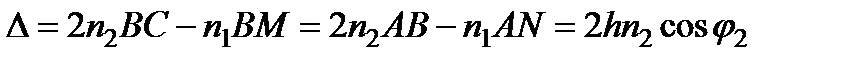а значит соответствующая разность фаз равна:

.

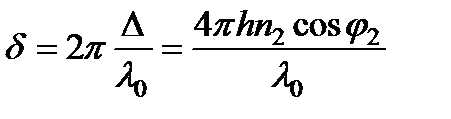Однако, дополнительная разность фаз, вызванная отражением, здесь отсутствует, так как оба внутренних отражения происходят в одинаковых условиях. Интерференционная картина, создаваемая протяженным источником, и в этом случае локализована в бесконечности.

Сравнивая и, видим, что картины в проходящем и отраженном свете будут дополнительными, т.е. светлые полосы одной и темные полосы другой будут находиться на одном и том же угловом расстоянии относительно нормали к пластинке. Кроме того, если отражательная способность R поверхности пластинки мала (например, на границе стекло-воздух при нормальном падении она примерно равна 0,04), то интенсивности двух интерферирующих лучей, прошедших сквозь пластинку, очень сильно отличаются друг от друга (I ₁/ I ₂ @ 1/ R ²~600), поэтому различие в интенсивности максимумов и минимумов (см. оказывается малым, а контрастность (видность) полос - низкой.

Наше предыдущее рассуждение было не вполне строгим. Так как мы пренебрегли многократностью внутренних отражений в пластинке. В действительности точки P достигает не две, как мы предполагали, а целый ряд пучков, идущих от S (лучи 3, 4 и т.д. на рис. 3.16 или 3.17).

Но если отражательная способность на поверхности пластинки мала, то наше предположение вполне удовлетворительно, так как пучки после первых двух отражений имеют ничтожную интенсивность. При значительной отражательной способности многократные отражения сильно изменяют распределение интенсивности в полосах, но положение полос, т.е. максимумов и минимумов, точно определяется формулами и.

Date: 2015-08-06; view: 767; Нарушение авторских прав