Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Понятие о пространственной когерентности
|
|
Если в предыдущем параграфе рассматривался точечный источник, но излучение его было не монохроматичным, то сейчас решим обратную задачу – источник монохроматичен, но имеет конечные размеры. Исследуем, как зависит качество интерференционной картины от размера источника.
Рассмотрим интерференцию, возникающую в результате выделения с помощью щелей S 1 и S 2 двух участков волнового фронта излучения от протяженного источника S. Его можно представить как сумму некогерентных между собой точечных источников.
Пусть u – текущая координата точки протяженного источника (рис. 3.12). Для простоты рассматриваем линейный источник. Как видно из рисунка, разность хода лучей от точки с координатой u до точки, характеризуемой координатой x равна: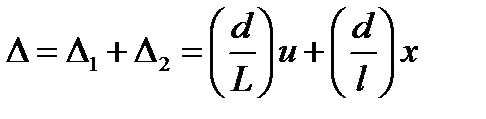 
,
а возникающая за счет этого разность фаз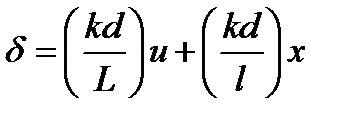 
Р и с. 3.12
Если J (u) du – интенсивность света, испущенного с участка источника длиной du и в точке источника с координатой u, то вклад от этого участка в полную интенсивность интерференционной картины в точке x выражается формулой: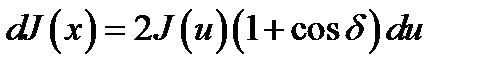 
,
где d задается равенством. Для полной интенсивности находим выражение:
.
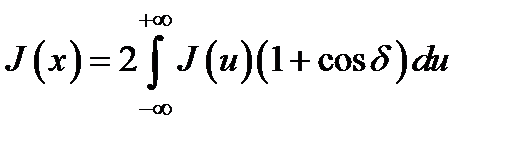Принимая во внимание, что
,
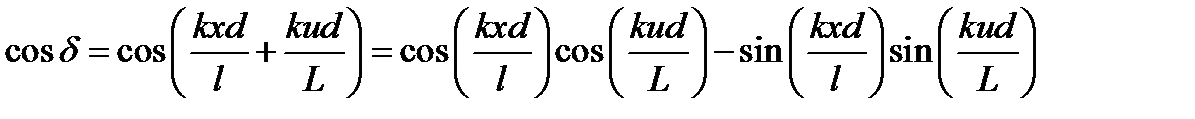представим в форме:
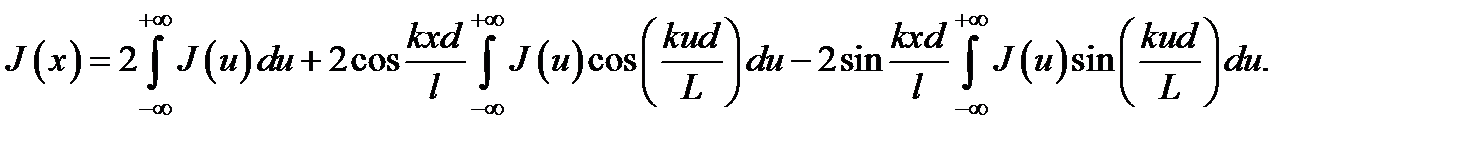
С помощью обозначений
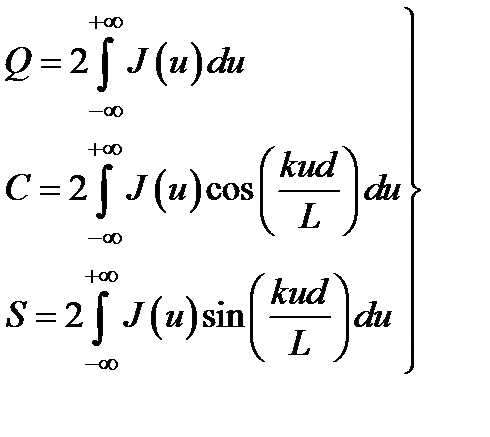
выражение можно записать аналогично тому, как это было представлено в предыдущем параграфе:
, где 
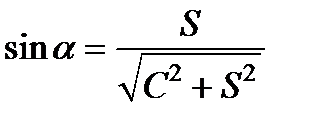
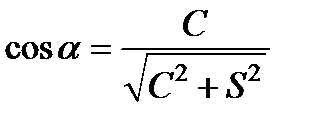. Следовательно, интенсивность опять изменяется по гармоническому закону, а максимумы и минимумы интенсивности соответственно равны: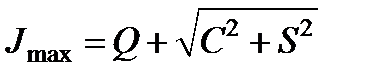 
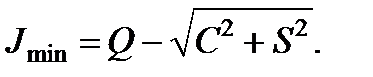Видимость представиться выражением: 
.
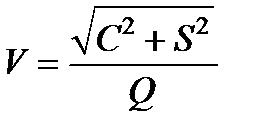Анализ интерференционной картины сводиться к вычислению интегралов Q, C, S.
Рассмотрим важный случай: источник с однородным распределением интенсивности излучения, когда функция J (u) задается формулой:
,
.
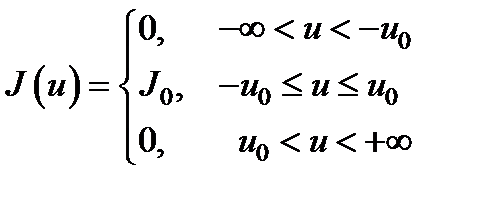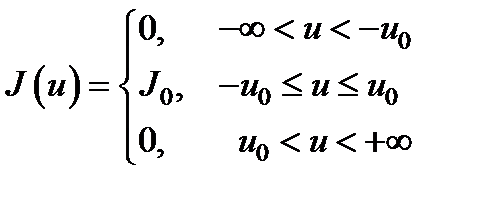График функции изображен на рис. 3.13.
Р и с. 3.13
По формулам находим:
,
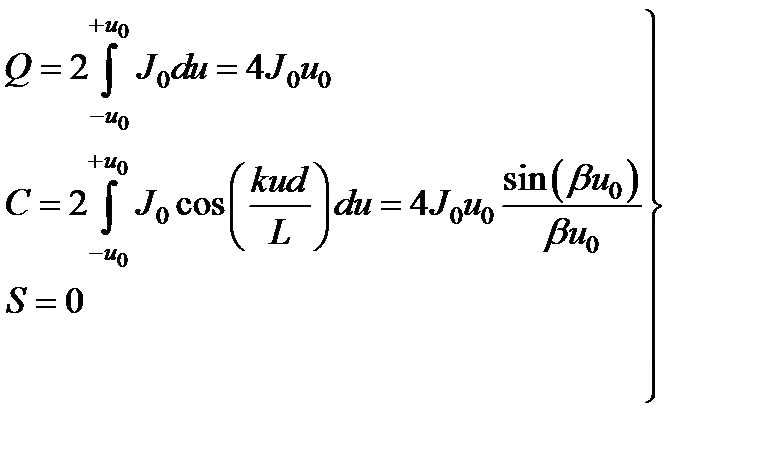где b = kd / L.
Следовательно, формула принимает вид:
.
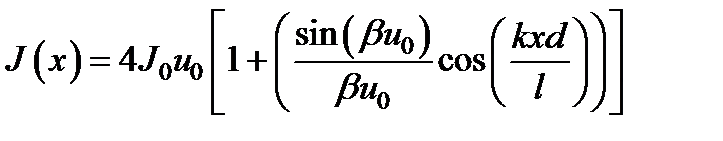В соответствии с и видимость выражается формулой:
.
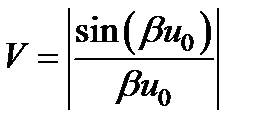Для точечного источника u 0 ® 0 и, следовательно, V ® 1. Источник, описываемый ступенчатой функцией, дает такие же интерференционные полосы, как и точечный источник, но их видимость уменьшается, т.е. видимость полос, согласно, зависит от размера источника.
Date: 2015-08-06; view: 549; Нарушение авторских прав