Гармонические колебания диполя

Вычислим энергетические характеристики излучения диполя, считая, что диполь совершает гармонические колебания с амплитудой A и с частотой w₀:

так что .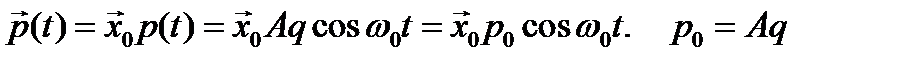

– единичный вектор, направленный вдоль линии, соединяющей заряды (рис. 2.7). Используя формулы и, получим ,

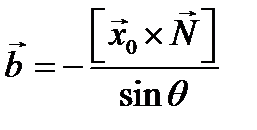– единичный вектор вдоль вектора .

Формулы, показывают, что излучение диполя линейно поляризовано, причем вектор лежит в плоскости векторов и 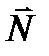, а вектор перпендикулярен этой плоскости (рис. 2.7).

Запишем вектор потока энергии .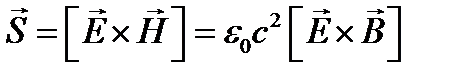

Учитывая формулы,, можно записать .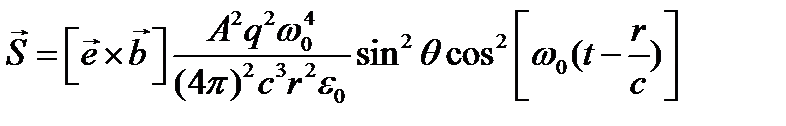

Из определения единичного вектора 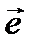следует, что

, т.к. , .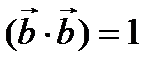

Поток энергии в волновой зоне

совпадает с направлением радиус-вектора (рис. 2.7). Усредняя выражение по времени, получаем интенсивность излучения диполя на расстоянии r .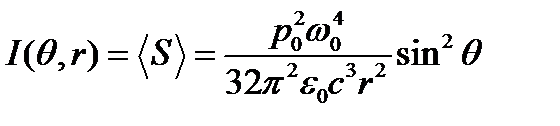

Зависимость интенсивности от направления выражается в множителем sin²q. Максимальная интенсивность наблюдается при q = p/2, т.е. в экваториальной плоскости: максимум интенсивности соответствует направлению, перпендикулярному оси диполя. Вдоль оси диполя (q = 0) энергия не излучается. Угловое распределение излучаемой осциллирующим диполем энергии показано на рис. 2.8. с помощью "диаграммы направленности". Длина отрезка, проведенного из начала координат до пересечения с линией r = sin²q, пропорциональна интенсивности распространяющейся в данном направлении волны. Распределение интенсивности по направлениям в пространстве характеризуется поверхностью, которая получается вращением кривой на рис. 2.8 вокруг оси OX.

Р и с. 2.8

Полную энергию, излучаемую диполем за 1 с по всем направлениям (мощность излучения) можно найти, вычисляя < S > через поверхность сферы радиусом r с центром в начале координат. Разобьем сферу на кольца координатными поверхностями q = const и q + d q = const. Площадь такого кольца равна 2p r ² sin q d q, а значение < S > во всех его точках можно считать одинаковым. Поэтому полная излучаемая мощность

.

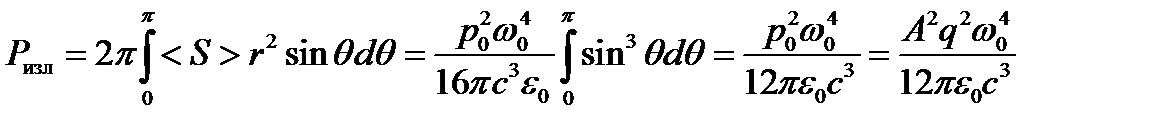Согласно формуле, излучаемая осциллятором мощность пропорциональна квадрату амплитуды его дипольного момента и четвертой степени частоты (обратно пропорциональна четвертой степени длины волны). Этот закон играет большую роль в теории рассеяния света. Короткие волны рассеиваются сильнее чем длинные. Этим объясняется голубой цвет неба и красный цвет Солнца на закате.

Выражаемый формулой поток излучения осциллятора через поверхность сферы не зависит от ее радиуса, т.е. через любую охватывающую осциллятор замкнутую поверхность протекает за 1 с одинаковая энергия. Этот факт объясняет характер зависимости напряженности электрического поля в формуле.

Date: 2015-08-06; view: 1107; Нарушение авторских прав