Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Периодические функции. Ряд Фурье. Дискретный спектр
|
|
Пусть некоторая функция времени f(t) является периодической, т.е. удовлетворяет условию
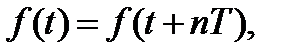
где t - произвольный момент времени, n - любое целое число, Т- период функции f(t). Типичный вид периодической функции показан на рис. 2.2, а.
Предположим, что функция f(t) кусочно-непрерывна и ограничена. Тогда, согласно теореме Дирихле, она может быть представлена в виде ряда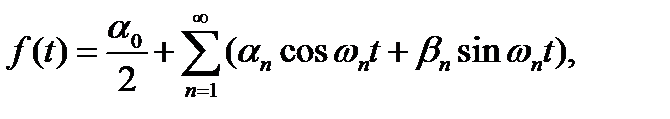 
где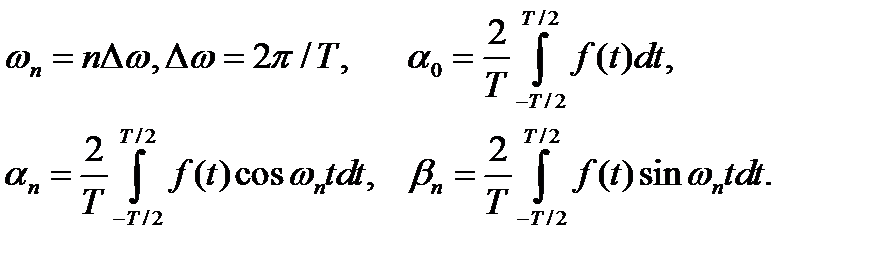 
Ряд называется рядом Фурье, а коэффициенты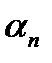 
и 
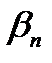- коэффициентами Фурье функции f(t). Индекс " n " в формуле нумерует частоты 
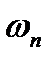составляющих функцию f(t) гармонических колебаний ("гармоник"). Как видно из формул, эти частоты разделены одинаковыми интервалами 
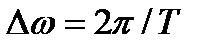и образуют эквидистантную последовательность.
Нетрудно убедиться в правильности формул для коэффициентов Фурье. Для этого достаточно умножить равенство на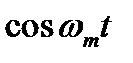 
или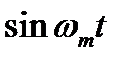 
, где m = 1,2,..., и проинтегрировать полученные соотношения по периоду функции f(t) от -Т/2 до Т/2. В математике доказывается единственность разложения. Тем самым математическая задача разложения периодических функций на гармонические колебания полностью решена.
| а) |
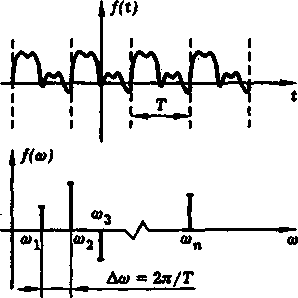
| б) |
Date: 2015-08-06; view: 470; Нарушение авторских прав