
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Спектральная амплитуда и спектральная фаза
|
|
Перепишем в виде 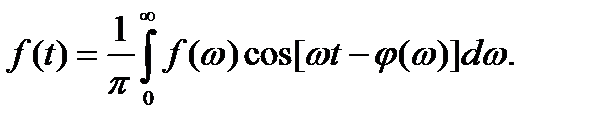 . Здесь
. Здесь 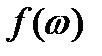 и
и  называются соответственно спектральной амплитудой и спектральной фазой функции f(t).
называются соответственно спектральной амплитудой и спектральной фазой функции f(t).
Пользуясь тригонометрической формулой 
преобразуем подынтегральное выражение в и приравняем его подынтегральному выражению в. Получим
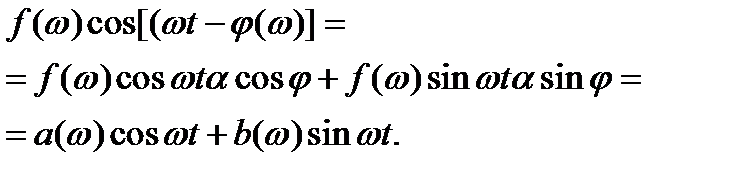
Приравнивая коэффициенты при функциях 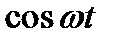 и
и 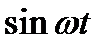 , находим связь между спектральными амплитудой и фазой с одной стороны и квадратурными компонентами
, находим связь между спектральными амплитудой и фазой с одной стороны и квадратурными компонентами 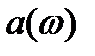 и
и 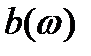 с другой:
с другой:
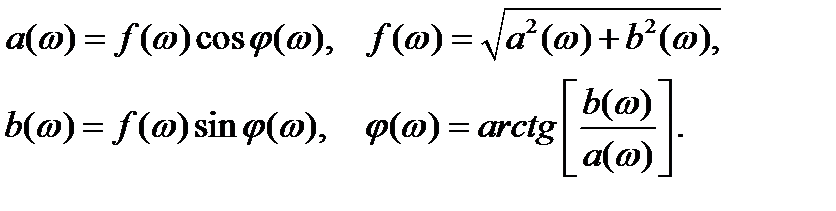
Обратим внимание на то, что непериодический процесс (в отличие от периодического) имеет сплошной спектр. Это следует из того, что спектральные характеристики процесса - 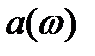 и
и 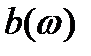 или
или 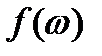 и
и 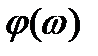 , определяемые формулами и - являются непрерывными функциями частоты. График спектральной амплитуды
, определяемые формулами и - являются непрерывными функциями частоты. График спектральной амплитуды 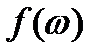 имеет вид непрерывной кривой (рис. 2.3). Таким образом, непериодическая функция - это суперпозиция гармоник, частоты которых изменяются непрерывно.
имеет вид непрерывной кривой (рис. 2.3). Таким образом, непериодическая функция - это суперпозиция гармоник, частоты которых изменяются непрерывно.
Итак, по виду спектра можно судить о характере самого процесса. Например, из того, что спектр солнечного света сплошной (цвета плавно переходят один в другой, между ними нет промежутков), можно сделать вывод, что излучение Солнца - непериодический процесс.
Из формул, определяющих квадратурные компоненты 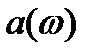 и
и 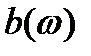 , видно, что
, видно, что 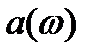 - четная функция частоты, а
- четная функция частоты, а 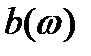 - нечетная:
- нечетная:
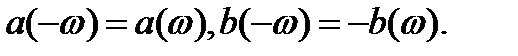
Поэтому можно переписать в симметризованном по 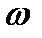 виде:
виде: 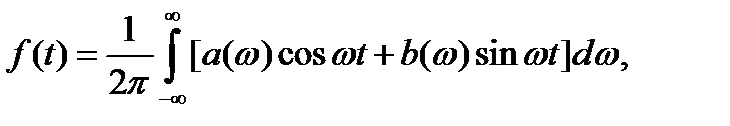
где функции 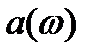 и
и 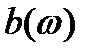 определены формулами.
определены формулами.
В мы впервые ввели отрицательные частоты, что позволило получить более симметричную запись преобразований Фурье, где все интегралы берутся теперь в бесконечных пределах. Подчеркнем, что отрицательные частоты введены формально математически. Содержание этого понятия полностью исчерпывается формулами
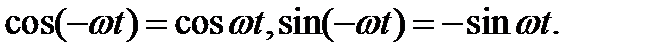
Никакого иного смысла термин "отрицательные частоты" не несет. Разумеется, на самом деле (физически) отрицательных частот не существует, так же как нет отрицательных периодов гармонических колебаний. Отрицательные частоты введены математически для удобства. Фактически они фигурируют только на промежуточных этапах расчетов, а в окончательные формулы для измеряемых физических величин никогда не входят.
Date: 2015-08-06; view: 931; Нарушение авторских прав