Непериодические функции. Интеграл Фурье. Сплошной спектр

Рассмотрим некоторую непериодическую функцию времени f(t) и попытаемся найти ее спектр (рис. 2.3).

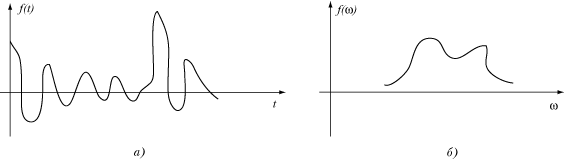
Р и с. 2.3.

С математической точки зрения непериодическую функцию можно рассматривать как периодическую с периодом, стремящимся к бесконечности. Поэтому для спектрального разложения непериодической функции f(t) нужно перейти к пределу 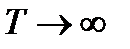в формулах,. Такой переход возможен, если функция f(t) удовлетворяет условию абсолютной интегрируемости

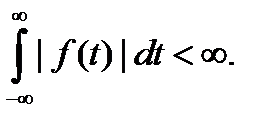
Используя выражение для 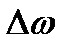, перепишем формулу в виде

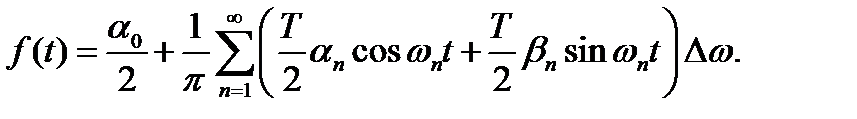
Теперь перейдем к пределу . При этом в силу формул (2.8) и (2.4) получаем

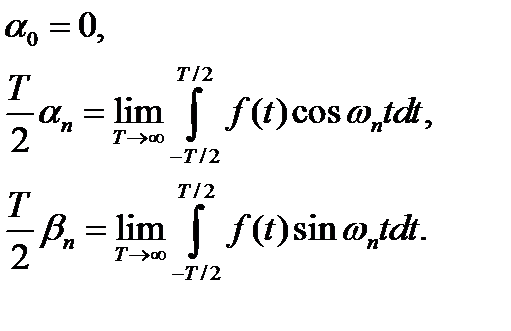
Поскольку , где 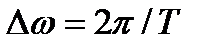, то в пределе при 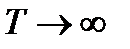частотный интервал 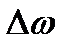стремится к нулю. При этом частота гармонических колебаний из дискретной переменной превращается в непрерывную переменную. Поэтому, опуская индекс " п " в, введем новые обозначения

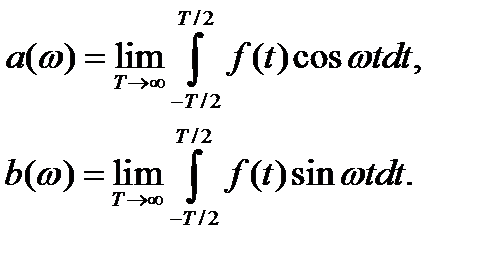
Наконец, переходя к пределу , 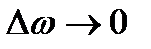в, заменяя предел суммы на интеграл и учитывая,, получаем

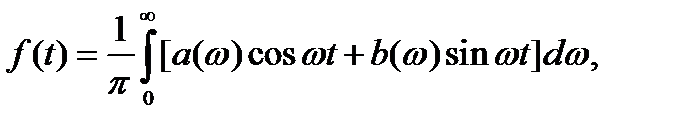где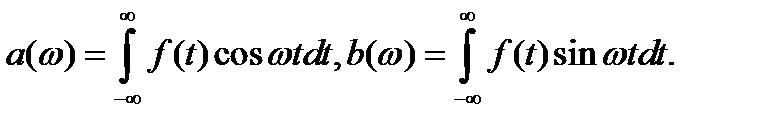

Интеграл называется интегралом Фурье.

Формулы, решают задачу о спектральном разложении непериодической функции времени. Выведем теперь несколько более компактных представлений для интеграла Фурье.

Date: 2015-08-06; view: 705; Нарушение авторских прав