Краткие теоретические сведения

Для выявления различий между двумя выборками с известным законом распределения применяют t-критерий различия Стьюдента. При этом предполагается, что данные распределены по нормальному закону. Критерий сравнивает средние двух выборок и вычисляет вероятность того, что они относятся к одной и той же генеральной совокупности. По вычисленной вероятности судят о принадлежности выборок к одной или разным совокупностям: если вероятность случайного появления значений в исследуемых выборках меньше уровня значимости α<0.05, то различия между выборками не случайны и они достоверно отличаются друг от друга.

Рассмотрим использование t-критерия Стьюдента для определения наличия различий между двумя выборками. При этом выборки могут быть:

- независимыми, несвязными (т.е. разные группы тестируемых) с разным числом значений в выборках – анализируют с помощью инструмента Двухвыборочный t-тест с различными дисперсиями или Двухвыборочный t-тест с одинаковыми дисперсиями;

- зависимыми, связанными (одна и та же группа тестируемых в разные моменты контроля, например, до обучения и после) с равным числом значений в выборках – анализируют с помощью инструмента Парный двухвыборочный t-тест для средних или Двухвыборочный t-тест с различными дисперсиями.

Отметим важность правильного подбора типа t-теста, поскольку для одних и тех же данных они могут давать разные результаты. Если выбор типа t-теста не очевиден, то правильным будет применение двухвыборочного t-теста с разными дисперсиями как общий случай анализа; если выборки зависимы и связаны, то применяют парный t-тест.

2. Использование Microsoft Excel и OpenOffice.org Calc
при определении достоверности различий между сравниваемыми группами

Включенная в Microsoft Excel функция ТТЕСТ для оценки отличий по t-критерия Стьюдента имеет параметр Тип для настройки на один из видов t -теста: 1 – парный тест, 2 - двухвыборочный t -тест с одинаковыми дисперсиями, 3 - двухвыборочный t-тест с разными дисперсиями. Аналогом данной функции в OpenOffice.org Calc является функция TTEST.

На рис. 82 приведены тестовые баллы по результатам тестирования двух групп обучаемых. Необходимо выявить достоверность различий в этих данных.

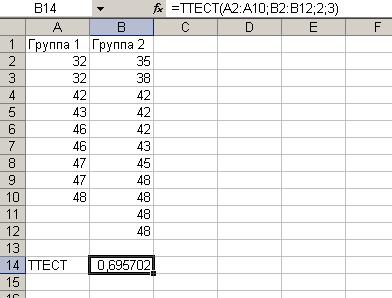
Рис. 82. Данные по результатам тестирования двух групп с рассчитанным значением t-критерия Стьюдента

В ячейку В14 введена функция ТТЕСТ из группы Статистические. На рис. 83 Массив1 – это диапазон данных Группы 1, Массив 2 – это диапазон данных Группы 2, Хвосты = 2, так как у нас двустороннее распределение; Тип =3, поскольку выборки не связаны, независимы и с разным числом значений.

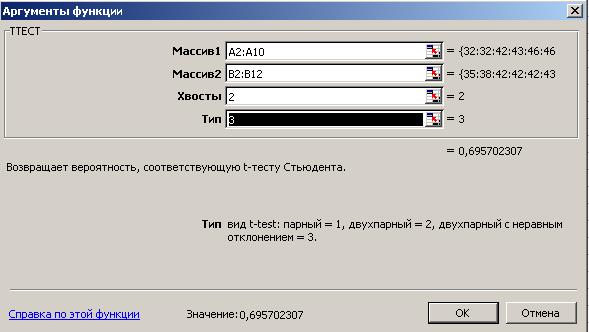
Рис. 83. Аргументы функции ТТЕСТ

Полученное с помощью функции ТТЕСТ значение величины случайного появления анализируемых выборок 0.6957 больше уровня значимости α=0.05. Таким образом, различия между выборками случайны и считаются не отличающимися друг от друга, что говорит о несущественности различий в двух группах испытуемых.

Аналогичные результаты в Microsoft Excel можно получить используя соответствующие инструменты Пакета анализа.

Date: 2015-07-27; view: 547; Нарушение авторских прав