
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Краткие теоретические сведения. Построение и дальнейший анализ одномерного распределения основывается на представлении данных в виде ряда распределения
|
|
Построение и дальнейший анализ одномерного распределения основывается на представлении данных в виде ряда распределения, который является исходным для применения большинства статистических методов.
В зависимости от вида вариации ряд может быть дискретным или интервальным.
Дискретный вариационный ряд – это ряд, значения вариантов которого выражены одним числом (значением признака).
Интервальный вариационный ряд это ряд, варианты которого выражены двумя числами (значениями признака), являющимися нижней и верхней границами интервала. Такие ряды обычно используются в случаях, когда число вариантов дискретного признака слишком велико, а также когда анализу подлежат вариации непрерывного признака. Интервалы в ряду могут быть как равными, так и неравными. Это зависит от характера статистических данных и задач исследования.
Вариационный ряд может быть асимметричным, т.е. таким, в котором наибольшей частотой обладают крайние значения вариант.
Частота – это величина, равная числу встречаемости признака в совокупности.
Частоты представляют собой абсолютный показатель распределения, а относительным показателем является частость (доля). Частость представляет собой отношение частоты встречаемости данного признака к сумме всех частот. Ее можно выражать как непосредственно в долях (тогда сумма частостей ряда будет равна единице), так и в процентах (тогда сумма частостей ряда будет равна 100%).
Примером дискретного ряда может служить распределение студентов по курсам:
| Курс | Количество студентов, чел. |
| 1-й | |
| 2-й | |
| 3-й | |
| 4-й | |
| 5-й | |
Графически эти данные можно отобразить в виде гистограммы (рис. 77).
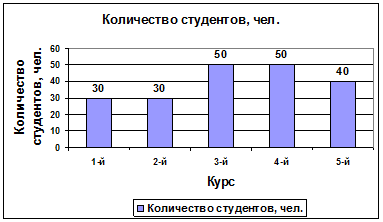
Рис. 77. Гистограмма распределения количества студентов
по курсам (дискретный вариационный ряд)
Визуальный анализ гистограмм позволяет выявить характер распределения данных и ответить на следующие шесть вопросов:
1. Какие значения типичны для заданного набора данных?
2. Как различаются между собой значения (диапазон значений)?
3. Сконцентрированы ли данные вокруг некоторого типичного значения?
4. Какой характер имеет эта концентрация данных? В частности, одинаков ли характер «затухания» для малых и больших значений данных?
5. Есть ли в заданном наборе такие значения, которые сильно отличаются от остальных и требуют специальной обработки (выбросы, т.е. такие значения, которые либо слишком велики, либо слишком малы.)?
6. Можно ли сказать, что в целом это однородный набор или отчетливо наблюдается наличие групп, которые надо анализировать отдельно?
Интервальный ряд распределения – это ряд, в котором значения признака заданы в виде интервала. Например, распределение студентов по младшим и старшим курсам можно представить в виде интервального ряда:
| Курс | Количество студентов, чел. |
| 1–2-й | |
| 3–5-й | |
При этом графическое представление интервального ряда в виде гистограммы представлено на рис. 78.

Рис. 78. Гистограмма распределения количества студентов
по курсам (интервальный вариационный ряд)
При определении интервальных рядов распределения необходимо определить, какое число групп следует образовать и какие взять интервалы (равные, неравные, закрытые, открытые).
При установлении количества интервалов можно воспользоваться следующей формулой: r» [1+3,2 lg(n)], (r – количество интервалов, n – количество данных). Для того чтобы вариационный ряд не был слишком громоздким, обычно число интервалов берут от 6 до 11.
2. Использование Microsoft Excel и OpenOffice.org Calc
при построении вариационных рядов
Таблица 22
Функции Microsoft Excel и OpenOffice.org Calc,
используемые для построения вариационных рядов
| Функция Excel (рус.) | Функция Calc (англ.) | Назначение |
| МАКС | MAX | Возвращает максимальное значение из списка аргументов |
| МИН | MIN | Возвращает наименьшее значение в списке аргументов |
| ЧАСТОТА | FREQUENCY | Возвращает распределение частот в виде вертикального массива. В Excel имеет формат ЧАСТОТА (массив_данных;массив_интервалов), в Calc: FREQUENCY(массив_данных;массив_интервалов) Массив_данных – это массив или ссылка на множество данных, для которых вычисляются частоты. Массив_интервалов – это массив или ссылка на множество интервалов, в которые группируются значения аргумента «массив_данных» |
| LOG10 | LG | Возвращает значение десятичного логарифма |
Date: 2015-07-27; view: 796; Нарушение авторских прав