Краткие теоретические сведения. Показатели, характеризующие центральную тенденцию (меры среднего уровня)

Показатели, характеризующие центральную тенденцию (меры среднего уровня).

Средняя представляет собой количественную характеристику качественно однородной совокупности. Наиболее распространенными средними являются средняя арифметическая, мода и медиана.

Средняя арифметическая (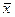) – обобщающий показатель, выражающий типичные размеры количественных признаков качественно однородных явлений, определяется по формуле:

,

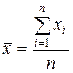где x_i – варианта с порядковым номером 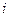( 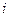=1,… n); n – объем совокупности.

Для интервального ряда используется средняя арифметическая взвешенная:

,

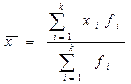где f_i – частота индивидуального значения признака;

k – количество градаций признака.

Мода (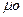) – варианта, которая чаще всего встречается в данном вариационном ряду. В интервальном ряду по определению можно установить только модальный интервал, при этом значение моды определяется по формуле:

,

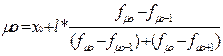где x₀ – нижняя граница модального интервала;

l – величина интервала;

f _μo – частота модального интервала;

f _μo–1 – частота предмодального интервала;

f _μo+1 – частота послемодального интервала.

Медиана (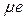) – варианта, находящаяся в середине вариационного ряда:

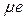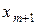= , если число вариант нечетно (n =2 m +1);

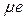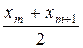= , если число вариант четно (n =2 m).

Медиана используется, когда изучаемая совокупность неоднородна. Особое значение она приобретает при анализе асимметричных рядов – она дает более верное представление о среднем значении признака, т.к. не столь чувствительна к крайним (нетипичным в плане постановки задачи) значениям, как средняя арифметическая.

Для интервального ряда можно определить как медианный интервал, а сама медиана рассчитывается по формуле:

,

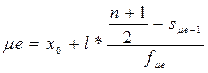где x ₀ – нижняя граница медианного интервала;

l – величина интервала;

n – количество единиц в совокупности;

s _{μe– 1} – накопленная частота предмедианного интервала;

f _μe – частота медианного интервала.

Меры центральной тенденции помогают при оценке качества теста в том случае, когда она проводится на репрезентативной выборке учеников.

Хороший нормативно-ориентированный тест обеспечивает нормальное распределение индивидуальных баллов учеников, когда среднее значение баллов совпадает с модой и находится в центре распределения, около 68% концентрируются вокруг среднего по нормальному закону, а остальные сходят на нет к краям распределения (нормальное распределение).

Показатели (меры), характеризующие рассеяние относительно центральной тенденции. Средние позволяют охарактеризовать статистическую совокупность одним числом, однако, не содержат информации о том, насколько хорошо они представляют эту совокупность. Для определения того, насколько сильно варьируются значения признака, используются такие характеристики, как размах вариации, дисперсия и среднее квадратическое отклонение.

Все они показывают, насколько сильно варьируют значения признака (а точнее – их отклонения от среднего) в данной совокупности. Чем меньше значение меры разброса, тем ближе значения признака у всех объектов к своему среднему значению, а значит, и друг к другу. Если величина меры разброса равна нулю, значения признака у всех объектов одинаковы.

Размах вариации (R) – это разность между наибольшим и наименьшим значениями признака:

,

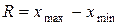где x_max – максимальное значение признака;

x_min – минимальное значение признака.

Показатель этот достаточно просто рассчитывается, однако является наиболее грубым из всех мер рассеяния, поскольку при его определении используются лишь крайние значения признака, а все другие просто не учитываются.

При расчете двух других характеристик меры вариации признака используются отклонения всех вариант от средней арифметической. Эти характеристики (дисперсия и среднее квадратическое отклонение) нашли самое широкое применение почти во всех разделах математической статистики.

Дисперсия (s ²) – абсолютная мера вариации (колеблемости) признака в статистическом ряду – средний квадрат отклонения всех значений признака ряда от средней арифметической этого ряда:

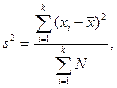
где x_i – варианта с порядковым номером ;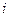

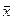– средняя арифметическая;

N – объем совокупности.

Дисперсия для вариационного ряда рассчитывается по формуле:

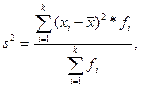
где 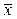– среднее значение признака;

x_i – индивидуальное значение признака;

f_i – общее число единиц наблюдения.

Низкая дисперсия индивидуальных баллов говорит о слабой дифференциации испытуемых по уровню подготовленности в группе, что противоречит основной цели нормативно-ориентированных тестов

Дисперсия выражает разброс в «единицах в квадрате» (например, в «балл в квадрате»). Для представления меры вариации в тех же единицах, что и варианты, используется среднее квадратическое (стандартное) отклонение, которое интерпретировать гораздо проще, т.к. выражается в привычных для нас единицах (например, в «баллах»).

Среднее квадратическое (стандартное) отклонение (s) – это квадратный корень из дисперсии:

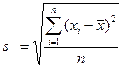или .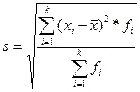

Стандартное отклонение показывает, насколько в среднем индивидуальные значения признака отличаются от среднего.

Рассмотренные меры рассеяния – абсолютные величины. Однако часто бывает необходимо сравнить вариацию одного и того же признака у разных групп объектов, выявить степень различия одного и того же признака у одной и той же группы объектов в разное время, сопоставить вариацию разных признаков у одних и тех же групп объектов. Для решения этих задач необходимо использовать относительные показатели. Таким показателем является коэффициент вариации.

Коэффициент вариации (V) – это отношение стандартного отклонения к средней арифметической, выраженное в процентах:

.

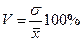Совокупность, составленная по результатам тестирования, считается однородной, если коэффициент вариации не превышает 35%.

Коэффициент вариации часто используют при проведении сравнений выборок различных объемов, например результатов тестирования разных по численности групп.

Следует отметить, что при ассиметричном (скошенном) распределении данных коэффициент вариации может превысить 100%. Такой результат означает, что в изучаемой ситуации наблюдается очень сильный разброс данных относительно среднего.

2. Использование Microsoft Excel и OpenOffice.org Calc
при вычислении выборочных характеристик

2.1. Использование инструмента Пакет анализа в Microsoft Excel

В пакете Microsoft Excel помимо мастера функций имеется набор более мощных инструментов для работы с несколькими выборками и углубленного анализа данных, называемый «Пакет анализа», который может быть использован для решения задач обработки выборочных данных.

Для установки пакета Анализ данных в Microsoft Excel сделайте следующее: выберите команду Надстройки; в появившемся списке установите флажок Пакет анализа.

Далее в диалоговом окне активируйте инструмент Описательная статистика, который предоставит рассчитанные значения основных статистических показателей.

2.2. Использование специальных функций

Ниже в табл. 27 приведены специальные функции анализа данных, используемые в рамках описательной статистики.

Таблица 27

Date: 2015-07-27; view: 607; Нарушение авторских прав