
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Применение метода наименьших квадратов при аппроксимации апериодических зависимостей
|
|
Часто экспериментальные зависимости заведомо описываются дифференциальными уравнениями первого порядка (например, нарастание тока в обмотках управления, нарастание давления в полостях силового цилиндра), решением которых являются экспоненты. По результатам экспериментальных измерений желательно определить параметры экспоненты. Для получения исходных данных необходимо провести эксперимент – подать на вход элемента скачек сигнала и записать реакцию на выходе.
Для упрощения расчетов желательно нормировать полученные экспериментальные данные: совместить начало процесса с началом координат, установившееся значение выходной величины принять равной 1. В этом случае мы будем искать аппроксимирующую зависимость в виде
G = 1 – e-kx,
или
G = 1 – e-(x/T) ,
здесь G - реакция системы, х - входной сигнал системы, k = 1/ T.
Как и ранее составим величину φ – сумму квадратов отклонений экспериментальных точек от экспоненты
φ = ∑(y i -1 + e-kxi )2.
Как и ранее для k следует выбирать такое значение, при котором φ имеет минимум, т.е.
dφ/dk = -2 ∑(y i -1 + e-kxi ) kx i = 0,
т.к. 2 ≠ 0, kx i ≠ 0, то (???e-kxi ≠ 0???),
то y i -1 + e-kxi = 0,
откуда
e-kxi = 1 - yi.
Если в последнем уравнении взять натуральный логарифм от левой и правой частей, то получим
- kx i = ln(1 – y i),
и далее
k = - (ln(1- y i))/ x i.
Если есть предположение, что рассматриваемый процесс может быть удобно описан экспонентой то по полученной формуле нужно определить 3 – 4 значения коэффициента k, затем определить среднее значение k. Предварительно нужно пронормировать экспериментальные данные как указывалось выше.
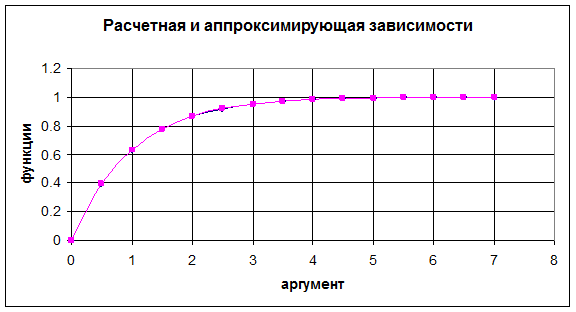
Примеры: Рассмотрим определение показателя для функции y = 1-e-x
В первом столбце таблицы приведены значения аргумента х, во втором столбце приведены рассчитанные значения функции у. Выберем на расчетном графике три точки:
1) хi = 0,5 yi = 0,39
k = - (ln(1- yi))/xi = - (ln(1- 0,39))/0,5 = - (ln0,61)/0,5 = - 2,303*log(0,61)/0,5= 0,99. (Примечание: log(0,61) – число отрицательное)
2) хi = 1 yi = 0,63
k = - (ln(1- yi))/xi = -(ln(1- 0,63))/1 = - (ln0,37)/1 = 2,303*log(0,37)/1 = 0,99.
3) хi = 6 yi = 0,998
k =- (ln(1- yi))/xi = (ln(1- 0,998))/6 = = - 2,303 (log (-0,002))/6= 1,04.
Примечание: число – 2,303 – модуль перехода от натуральных логарифмов к десятичным.
Определяем среднее значение k.
k = (0,99 + 0,99 + 1,04)/3 = 1,006.
С полученным показателем степени строится график по данным третьего столбца. В пределах точности построения оба графика совпали.
| k = 1 | k = 1.006 | |
| 0.5 | 0.393469 | 0.395286 |
| 0.632121 | 0.634321 | |
| 1.5 | 0.77687 | 0.778869 |
| 0.864665 | 0.866279 | |
| 2.5 | 0.917915 | 0.919137 |
| 0.950213 | 0.951101 | |
| 3.5 | 0.969803 | 0.97043 |
| 0.981684 | 0.982119 | |
| 4.5 | 0.988891 | 0.989187 |
| 0.993262 | 0.993461 | |
| 5.5 | 0.995913 | 0.996046 |
| 0.997521 | 0.997609 | |
| 6.5 | 0.998497 | 0.998554 |
| 0.999088 | 0.999126 |
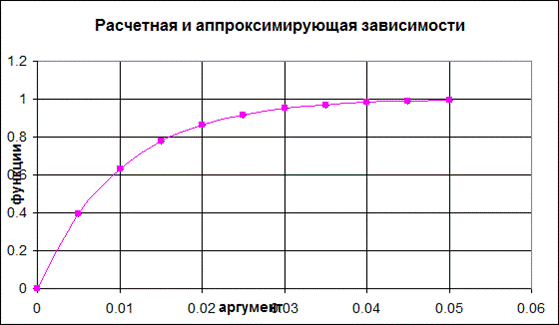
Пример 2: Рассмотрим определение показателя для функции
y = 1-e-0.01x . В первом столбце таблицы приведены значения аргумента х, во втором столбце приведены рассчитанные значения функции у. Выберем на расчетном графике три точки:
| k=100 | K=100,1 | |
| 0.005 | 0.393469 | 0.393773 |
| 0.01 | 0.632121 | 0.632488 |
| 0.015 | 0.77687 | 0.777204 |
| 0.02 | 0.864665 | 0.864935 |
| 0.025 | 0.917915 | 0.91812 |
| 0.03 | 0.950213 | 0.950362 |
| 0.035 | 0.969803 | 0.969908 |
| 0.04 | 0.981684 | 0.981757 |
| 0.045 | 0.988891 | 0.988941 |
| 0.05 | 0.993262 | 0.993296 |
1) хi = 0,005 yi = 0,4
k = - (ln(1- yi))/xi = -(ln(1- 0,4))/0,005 = - 2,303(lg 0,6)/0,005= 102,3.
2) хi = 0,015 yi = 0,777
k = - (ln(1- yi))/xi = -(ln(1- 0,777))/0,015 = - 2,303(lg 0,222)/0,015 = 100,1.
3) хi = 0,025 yi = 0,918
- (ln(1- yi))/xi = (ln(1- 0,918))/0,025 = = - 2,303(lg(0,082))/0,025= 100,1.
Определяем среднее значение k.
k = (102, 3 + 100,1 + 100,1)/3 = 100,8.
С полученным показателем степени строится график по данным третьего столбца. В пределах точности построения опять оба графика совпали.
Date: 2015-07-27; view: 796; Нарушение авторских прав