Метод наименьших квадратов. Если некоторая физическая величина зависит от другой величины, то эту зависимость можно исследовать

Если некоторая физическая величина зависит от другой величины, то эту зависимость можно исследовать, измеряя y при различных значениях x. В результате измерений получается ряд значений:

x₁, x₂,..., x_i,,..., x_n;

y₁, y₂,..., y_i,,..., y_n.

По данным такого эксперимента можно построить график зависимости y = ƒ(x). Полученная кривая дает возможность судить о виде функции ƒ(x). Однако постоянные коэффициенты, которые входят в эту функцию, остаются неизвестными. Определить их позволяет, как говорилось выше, метод наименьших квадратов. Экспериментальные точки, как правило, не ложатся точно на кривую. Метод наименьших квадратов требует, чтобы сумма квадратов отклонений экспериментальных точек от кривой, т.е. [y_i – ƒ(x_i)]² была наименьшей.

На практике этот метод наиболее часто (и наиболее просто) используется в случае линейной зависимости, т.е. когда

y = kx или y = a + bx.

Линейная зависимость очень широко распространена в практике испытаний. И даже когда зависимость нелинейная, обычно стараются строить график так, чтобы получить прямую линию.

Рассмотрим зависимость y = kx (прямая, проходящая через начало координат). Составим величину φ – сумму квадратов отклонений наших точек от прямой

.

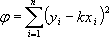Величина φ всегда положительна (т.к квадрат) и оказывается тем меньше, чем ближе к прямой лежат наши точки. Метод наименьших квадратов утверждает, что для k следует выбирать такое значение, при котором φ имеет минимум, т.е.

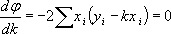
откуда

Рассмотрим теперь несколько более трудный случай, когда точки должны удовлетворить формуле y = a + bx (прямая, не проходящая через начало координат).

Задача состоит в том, чтобы по имеющемуся набору значений x_i, y_i найти наилучшие значения a и b.

Снова составим квадратичную форму φ, равную сумме квадратов отклонений точек x_i, y_i от прямой

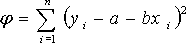
и найдем значения a и b, при которых φ имеет минимум

;

.

.

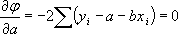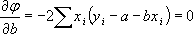Совместное решение этих уравнений дает

.

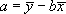Date: 2015-07-27; view: 808; Нарушение авторских прав