Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






Погрешности косвенных измерений. При обработке результатов косвенных измерений физической величины, связанной функционально с физическими величинами А

⇐ ПредыдущаяСтр 9 из 33Следующая ⇒

 

При обработке результатов косвенных измерений физической величины, связанной функционально с физическими величинами А, В и С, которые измеряются прямым способом, сначала определяют относительную погрешность косвенного измерения e= DХ/Хпр, пользуясь формулами, приведенными в таблице (без доказательств).

Абсолютную погрешность определяется по формуле DХ=Хпр *e,

где e выражается десятичной дробью, а не в процентах.

Окончательный результат записывается так же, как и в случае прямых измерений.

Вид функции Формула
Х=А+В+С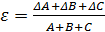    
Х=А-В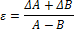      
Х=А*В*С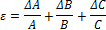  
  Х=Аn
Х=А/В    
Х=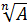  

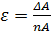
Пример: Вычислим погрешность измерения коэффициента трения с помощью динамометра. Опыт заключается в том, что брусок равномерно тянут по горизонтальной поверхности и измеряют прикладываемую силу: она равна силе трения скольжения.

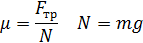
С помощью динамометра взвесим брусок с грузами: 1,8 Н. Fтр=0,6 Н

μ=0,33. Инструментальная погрешность динамометра (находим по таблице) составляет Δ и = 0,05Н, Погрешность отсчета (половина цены деления) Δ о =0,05Н. Абсолютная погрешность измерения веса и силы трения 0,1 Н.

Относительная погрешность измерения (в таблице 5-я строчка)

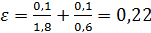, следовательно, абсолютная погрешность косвенного измерения μ составляет 0,22*0,33=0,074

Ответ: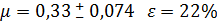

Вычисление погрешностей. В дальнейшем будем предполагать, что

.

Таблица 1. Коэффициенты Стьюдента.
a =0,68 a =0,95 a =0,99
n ta,n n ta,n n ta,n
  2,0   12,7   63,7
  1,3   4,3   9,9
  1,3   3,2   5,8
  1,2   2,8   4,6
  1,2   2,6   4,0
  1,1   2,4   3,7
  1,1   2,4   3,5
  1,1   2,3   3,4
  1,1   2,3   3,3
  1,1   2,1   3,0
  1,1   2,1   2,9
  1,1   2,0   2,8
  1,0   2,0   2,6

 

 Смысл понятий "доверительный интервал" и "доверительная вероятность" состоит в следующем: пусть a =0.95, тогда можно утверждать с надежностью 95%, что истинное значение величины xист не отличается от оценки (3) больше, чем на ± D xсл . Значения коэффициентов ta ,n в зависимости от a и n табулированы (см. табл. Чтобы окончательно установить границы доверительного интервала необходимо расширить его с учетом систематической погрешности D xсист. Систематическая погрешность, как правило, указана в паспорте или на шкале прибора, а в простейших случаях может быть принята равной половине цены деления младшего разряда шкалы. Обычно (хотя, строго говоря, и неверно) суммарная погрешность определяется как корень квадратный из суммы квадратов случайной и систематической погрешностей:

 

.


⇐ Предыдущая45678910111213Следующая ⇒





Date: 2015-07-27; view: 2529; Нарушение авторских прав


mydocx.ru - 2015-2025 year. (0.007 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию