Некоторые понятия математической статистики

В.А.Чащин

ТЕХНОЛОГИЯ ИСПЫТАНИЙ МЕХАНИЗМОВ ПРИВОДОВ

Конспект лекций

Москва

Технология испытаний механизмов приводов

Курс читается в 10-м семестре.

Состав курса:

Лекции – 34 часа, (17 лекций)

Лаб.раб. – 16 час (4*4).

Курсовая работа – 1.

Групп – 3.

Отчетность – зачет.

Литература к курсу:

1. Мильграм Ю.Г., Слабкин Л.И. Основы экспериментальных исследование (Техника физического эксперимента и статистические основы экспериментальных исследований)/ Под ред. Ю.Г. Мильграма. ВВИА им. Н.Е. Жуковского. 1983 г. 404 с.

2. Льюнг Л. Идентификация систем. Теория для пользователя. – М. Наука. 1991 г. 432 с.

3. Бутко Г. И., Ивницкий В.А., Порывкин Ю.П. Оценка характеристик систем управления летательными аппаратами. – М.: Машиностроение, 1983. – 272 с.

4. Сапожников В.М. Монтаж и испытания гидравлических и пневматических систем летательных аппаратов.

5. Болтон У. Карманный справочник инженера-метролога. –М.: Издательский дом «Додека-XXI», 2002.-384 с.

Испытания приводов

Общие положения

В процессе разработки изделия проводятся различны испытания. Например, серийно изготовленные приводы подвергаются следующим видам стендовых испытаний: приемо-сдаточным, периодическим, проверочным (технологическим), ресурсным. На ранних стадиях разработки изделий проводятся достаточно большое количество испытаний с целью уточнения расчетной и математической модели изделия или его входящих узлов. Испытания в лабораторном практикуме по учебному курсу ближе к испытаниям по качественной проверке моделей элементов привода и самого привода. В процессе разработки изделия возможно проведение испытаний для уточнения модели устройства. Вернее сказать по качественному подтверждению модели устройства, излагаемой в лекциях.

Некоторые понятия математической статистики

Математическая статистика – наука, занимающаяся разработкой методов получения, описания и анализа опытных данных (наблюдений, измерений). Основной задачей математической статистики является задача изучения закономерностей случайных массовых явлений, содержащихся в результатах наблюдений.

В математической статистике часто исследуют определенный признак, присущий большой группе однотипных объектов или изделий. Совокупность значений рассматриваемого признака у всех N объектов или изделий, где N предполагается большим, называется генеральной совокупностью. Выборкой называется совокупность n случайно отобранных объектов или изделий из всего множества N объектов, образующих генеральную совокупность. Числа N и n соответственно называются объемом генеральной совокупности и объемом выборки. Ясно, что чем больше объем выборки, тем, в общем случае, будут обоснованнее наши суждения о свойствах генеральной выборки, если только измерения являются независимыми. Выборка должна обладать репрезентативным (представительным) свойством. Для этого нужно обеспечить при составлении выборки равную вероятность попасть в нее любому объекту из генеральной совокупности. Если это имеет место, то говорят, что выборка осуществляется случайно.

Выборку можно осуществлять:

-бесповторным и повторным образом,

-простым отбором (последовательное извлечение объектов из генеральной выборки),

-механическим образом (генеральная совокупность механически делится на группы, а из них случайно выбираются объекты). Например, если нужно отобрать 10% всех изделий, то следует в выборку включить каждое 10-е изделие. И рядом других способов.

На практике в вопросах математической статистики вместо вероятности P(A) вводится частость W(A) появления случайной величины.

W(A) называется статистической вероятностью, P(A) – называется теоретической вероятностью. При увеличении числа испытаний частость приближается к вероятности.

Результаты последовательности измерений одной и той же величи-ны могут быть построены в виде графика их частотного распределения. Параметр «частота» показывает количество появлений некоторого значения или значений измеряемой величины внутри диапазона всех значений. Построенная зависимость (см. ниже) частоты появления значений от самой измеряемой величины и есть частотное распределение. Чем шире это распределение, тем меньше точность измерений.

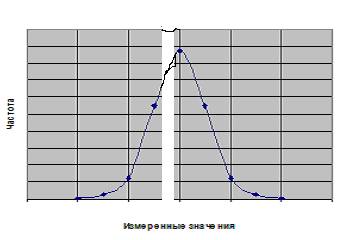
При измерениях пользуются рядом понятий. Среднее арифметическое значение (x ‾). Это сумма всех результатов измерений, деленная на количество рассматриваемых измерений

.

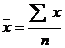Оценка точности или разброса частотного распределения проводится при помощи среднеквадратичного отклонения (стандартного отклонения). Отклонение (d) – это разность между средним и полученным значениями. Сумма квадратов полученных отклонений (∑ d ²), деленная на количество измерений n, дает среднее значение квадратов отклонений. Квадратный корень из этого значения и есть среднеквадратичное отклонение σ

σ = √(∑(d ²/ n)).

Частотное распределение серии измерений показывает отклонения, т.е. погрешности, результатов измерений от среднего значения. Частотное распределение обычно отображается в виде графика

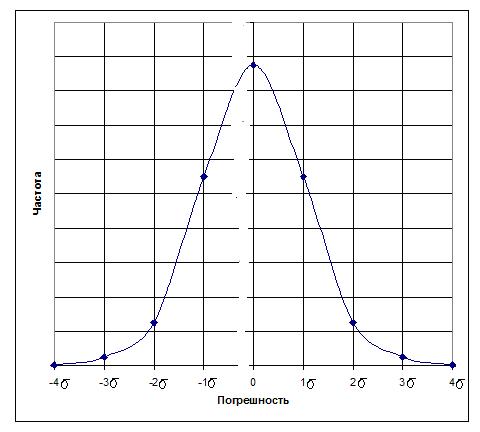
Это представление называется нормальным распределением Гаусса. Такое распределение показывает, что наиболее часто встречающееся значение измеряемой величины, у которого нет погрешности измерения и есть среднее значение, что малая погрешность имеет большую вероятность, чем большая и что график симметричен относительно среднего значения.

Из распределения Гаусса видно, что вероятность попадания результата измерения в интервал одного стандартного отклонения от среднего значения равна 68,3%, в интервал двух стандартных отклонений – 95,5%, в интервал трех стандартных отклонений – 99,7%, а четырех – 99,99%. Вероятность попадания результата измерения в интервал, составляющий ±0,674σ от среднего значения, равна 50%. Интервал 0,674σ называется вероятной погрешностью.

Date: 2015-07-27; view: 607; Нарушение авторских прав