Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Естественные координатные оси и их орты
|
|
Пусть заданы траектория точки, начало и направление отсчета дуг. Выберем на траектории произвольным образом точку М и проведем касательную 
. Плоскость, проходящая через точку М перпендикулярно к касательной 
, называется нормальной плоскостью траектории в точке М (рис. 84).
Придадим дуговой координате s приращение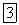 
и отметим точку 
с координатой 
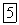. Пусть 
- касательная к траектории в точке 
. В общем случае траектория точки - пространственная кривая, поэтому касательные 
и 
суть скрещивающиеся прямые.
Рис. 83.
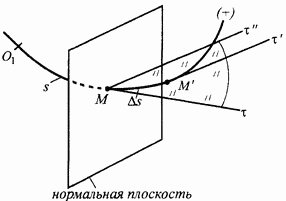
Рис. 84.
Проведем прямую 
, параллельную касательной 
. Прямые 
и 
образуют плоскость 
. Предельное положение плоскости 
, когда точка 
неограниченно приближается к точке М, называется соприкасающейся плоскостью траектории в точке М Соприкасающаяся плоскость представляет собой ту из бесконечного множества плоскостей, проходящих через касательную 
, которая наиболее тесно примыкает к траектории в окрестности точки М. В случае плоской траектории соприкасающаяся плоскость совпадает с плоскостью траектории.
Нормальная и соприкасающаяся плоскости взаимно перпендикулярны. Проведем через точку М третью плоскость, перпендикулярную к обеим указанным плоскостям - так называемую спрямляющую плоскость. В итоге получаем прямой трехгранный угол с вершиной в точке М, называемый естественным трехгранником траектории в этой точке. Ребрами естественного трехгранника являются касательная 
, главная нормаль 
- линия пересечения нормальной и соприкасающейся плоскостей и бинормаль (вторая нормаль) 
- линия пересечения нормальной и спрямляющей плоскостей (рис. 85).
Касательная, главная нормаль и бинормаль взаимно перпендикулярны и после установления на них направлений образуют естественную систему координатных осей. Положительное направление касательной выбирается в сторону возрастания дуговой координаты s и задается ортом касательной 
. Положительное направление главной нормали задается ортом 
, который направляют от точки М в сторону вогнутости траектории. 
бинормали выбирают согласно правилу 
, чем обеспечивается правосторонность естественного координатного базиса 
(см. рис. 85).
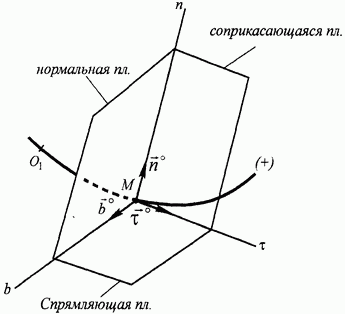
Рис. 85
Date: 2015-07-27; view: 405; Нарушение авторских прав