Способы задания движения точки

Различают векторный, координатный и естественный (натуральный) способы задания движения.

Векторный способ задания движения состоит в следующем.

Пусть М - движущаяся точка, А - тело отсчета (рис. 72). Выберем в теле А произвольную точку О - точку отсчета, построим вектор . Этот вектор, начало которого совпадает с точкой отсчета О, а конец - с точкой М называется радиусом-вектором точки М. При движении точки М радиус-вектор непрерывно изменяется во времени, поэтому существует некоторая вектор-функция времени

Если эта функция известна, то для каждого момента времени t может быть построен вектор 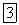и тем самым найдено положение движущейся точки в этот момент.

Функция (1) называется векторным законом (векторным уравнением) движения точки М.

При координатном способе задания движения с телом отсчета связывается какая-либо, например декартова прямоугольная, система координат (рис. 73).

Движение точки будет задано, если ее координаты будут известны как функции времени Рис. 72

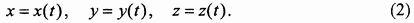
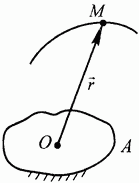
Рис. 72.

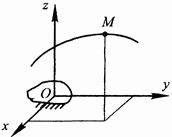
Рис. 73.

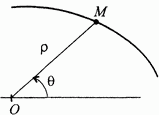
Рис. 74.

Зависимости (2), выражающие текущие координаты движущейся точки в виде функций времени, называются уравнениями движения точки в декартовых координатах.

Если точка движется, оставаясь все время в одной плоскости, то оси можно расположить в той же плоскости и ограничиться двумя уравнениями движения

При движении в плоскости часто удобно пользоваться полярной системой координат, задавая положение точки ее полярным углом 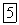и полярным радиусом (рис. 74). В этом случае уравнения движения точки имеют вид

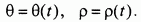
Линия, описываемая движущейся точкой в пространстве, называется траекторией точки. Естественный способ задания движения состоит в задании траектории точки и закона движения по траектории.

Пусть траектория точки М суть заданная кривая, М - положение точки на ней (рис. 75). Будем рассматривать траекторию как криволинейную координатную ось, для чего выберем на ней начало отсчета (точку ) и направление отсчета дуг (на рис. 75 направление отсчета выбрано вправо от точки ). Длина дуги , взятая со знаком плюс или минус в зависимости от положения точки М относительно начала отсчета , вполне определяет положение точки в пространстве и называется дуговой координатой точки. Движение точки будет задано, если ее дуговая координата 5 будет выражена в виде функции времени

Зависимость (4) называется законом движения точки по траектории или, что то же самое, законом движения точки в естественной форме.

Рис. 75.

Пример.

Написать уравнения движения точки, движущейся равномерно по окружности радиуса R и делающей n оборотов за одну минуту.

Начнем с естественного способа описания движения. Изображаем траекторию- окружность радиуса R с центром в точке О (рис. 76). Начало отсчета дуг совместим с положением точки в момент начала наблюдения, то есть при ; за положительное направление отсчета выберем направление в сторону движения точки.

Пусть М положение движущейся точки в текущий момент времени . Для центрального угла , который будем отсчитывать в сторону движения точки, согласно условию, можем написать

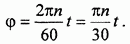
Здесь измеряется в радианах, t - в секундах.

Длина s дуги , радиус окружности R и центральный угол связаны геометрическим соотношением

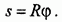
Подставляя сюда найденное значение , получаем

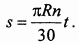
Это и есть закон естественной форме.

Для описания движения в координатной форме прежде всего следует выбрать подходящую систему координат, например, изображенную на рис. 77. Далее строят координатные отрезки и определяют соответствующие переменные расстояния. В нашем случае будем иметь:

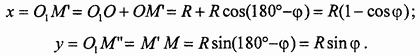
Подставляя сюда угол как функцию времени, получаем уравнения движения в координатной форме

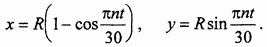
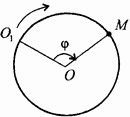
Рис. 76.

движения точки в

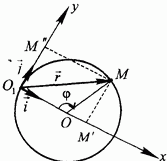
Рис. 77.

Пусть - координатные орты. Тогда для радиуса-вектора точки будем иметь:

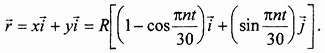
Полученное равенство, выражающее радиус-вектор точки М как функцию времени, служит векторным уравнением ее движения.

Date: 2015-07-27; view: 917; Нарушение авторских прав