Определение траектории, скорости и ускорения точки при векторном способе задания движения

Пусть движение точки М задано векторным способом, то есть задан радиус-вектор точки как функция времени

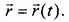
Линия, описываемая концом переменного вектора, начало которого находится в заданной неподвижной точке, называется годографом этого вектора. Отсюда и из определения траектории следует правило: траектория точки есть годограф ее радиуса-вектора.

Пусть в некоторый момент t точка занимает положение М и имеет радиус-вектор , а в момент - положение и радиус-вектор (рис. 78).

Вектор , соединяющий последовательные положения точки в указанные

Рис. 78.

моменты, называется вектором перемещения точки за время . Вектор перемещения следующим образом выражается через значения вектор-функции (5):

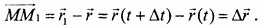
Если вектор перемещения поделить на величину промежутка , получим вектор средней скорости точки за время

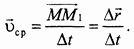
Будем теперь уменьшать промежуток , устремляя его к нулю. Предел, к которому стремится вектор средней скорости при неограниченном уменьшении промежутка , называется скоростью точки в момент t или просто скоростью точки 0. В соответствии со сказанным для скорости получаем:

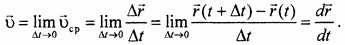
Итак, вектор скорости точки равен производной по времени от ее радиуса-вектора:

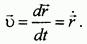
Поскольку секущая в пределе (при ) переходит в касательную , приходим к выводу, что векторскорости направлен по касательной к траектории в сторону движения точки.

В общем случае скорость точки также переменна, и можно интересоваться быстротой изменения скорости. Скорость изменения скорости называется ускорением точки.

Для определения ускорения а выберем какую-либо неподвижную точку А и будем откладывать из нее векторскорости и в различные моменты времени.

Линия, которую опишет конец N вектора скорости, представляет собой годограф скорости (рис. 79). Изменение вектора скорости выражается в том, что геометрическая точка N движется по годографу скорости, а скорость этого движения служит, по определению, ускорением точки М.

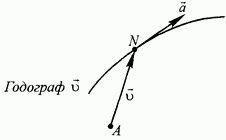
Рис. 79.

Применив для переменного вектора все те рассуждения, которые были использованы выше для переменного вектора , для ускорения получаем:

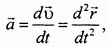
или, при обозначении производной по времени точкой:

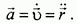
Формулы (6) - (8) являются наиболее общими формулами кинематики для определения скорости и ускорения.

Date: 2015-07-27; view: 529; Нарушение авторских прав