Интегральные формулы для координат центра тяжести

Для сплошных тел полученные приводятся к интегральному виду.

Тело называется сплошным, если вещество в теле распределено непрерывно. В сплошном теле можно неограниченно уменьшать размеры выделенных материальных элементов и осуществлять предельные переходы. Пусть массы и объемы элементов, выделенных в сплошном теле, - точки внутри этих элементов. Отношение 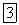называется средней плотностью тела в точке . Предел, к которому стремится средняя плотность при неограниченном уменьшении объема 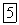, называется плотностью тела в точке :

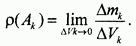
Тело называется однородным, если его плотность одинакова во всех точках: .

Для сплошных однородных тел, полагая , ( - ускорение силы тяжести) и переходя в формулах для координат центра тяжести к пределу при , получим:

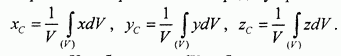
В этих формулах объем тела, объем выделенного элемента интегрирования, х, у, z — декартовы координаты какой-либо точки внутри или на границе элемента. Знак обозначает интегрирование по всему объему тела.

Для однородных поверхностных тел (мембраны, оболочки) и материальных линий (стержни, нити) эти формулы преобразуются к следующему виду:

для поверхностных тел

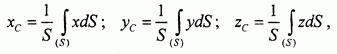
для материальных линий

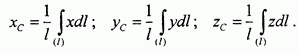
В этих формулах S - площадь поверхности тела, -площадь выделенного на ней элемента интегрирования, - длина линии, - длина ее элемента, х, у, z - декартовы координаты какой-либо точки, принадлежащей элементу интегрирования, - декартовы координаты центра тяжести данного поверхностного тела или материальной линии.

Пример 1.

Найти центр тяжести однородного полушара радиуса .

Выберем начало координат в центре основания полушара, проведем координатные оси (рис. 59). Полушар симметричен относительно оси , поэтому его центр тяжести С лежит на этой оси: . Остается определить величину .

В качестве элемента интегрирования выбираем в полушаре слой толщиной и круглым основанием радиуса . Далее находим (с точностью до величин первого порядка малости относительно ):

Подставляя найденные значения в интегральную формулу для координаты , вычисляем

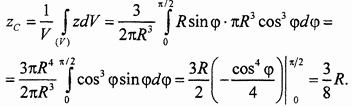
Таким образом, центр тяжести однородного полушара находится на его оси симметрии на расстоянии над центром основания.

Пример 2.

Найти центр тяжести дуги АВ окружности с радиусом R и центральным углом (рис. 60).

Поместим начало координат в центр соответствующей окружности, ось проведем через середину дуги, оси - перпендикулярно к ней. По теореме о положении центра тяжести симметричного тела будем иметь Координату вычисляем по соответствующей формуле для координат центра тяжести материальной линии.

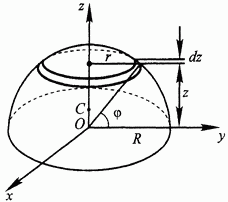
Рис. 59.

Примем за элемент интегрирования бесконечно малый участок дуги, определяемый конечным углом и бесконечно малым углом . Будем иметь: ( длина дуги АВ). Далее вычисляем :

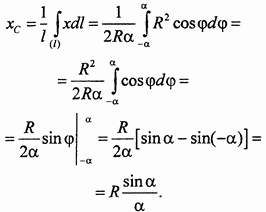
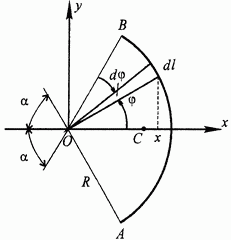
Рис. 60.

В этой формуле a выражается в радианах.

Придавая углу значение найдем абсциссу центра тяжести полуокружности:

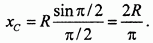
Аналогичным образом могут быть найдены центры тяжести других тел простой геометрической формы - отрезка прямой, площади треугольника, площади кругового сектора, объема конуса и т.д. А как быть в более сложных случаях? Из вычислительных способов (существуют еще экспериментальные способы) часто можно воспользоваться методом разбиения.

Date: 2015-07-27; view: 421; Нарушение авторских прав