
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Примечания
|
|
1. Если в минусовых клетках построенного цикла находится два (или несколько) одинаковых минимальных значения хij, то при перераспределении объемов груза освобождаются две (или несколько) клеток и план становится вырожденным. Для продолжения решения необходимо одну или несколько освобождающихся клеток таблицы занять нулем, причем предпочтение отдается клетке с наименьшим тарифом. Нулей вводится столько, чтобы во вновь полученном опорном плане число занятых клеток было равно (m+n-1).
2. Если в оптимальном плане транспортной задачи оценка свободной клетки равна нулю (∆ij=0), то задача имеет множество оптимальных планов. Для клетки с нулевой оценкой можно построить цикл и перераспределить груз. В результате полученный оптимальный план будет иметь такое же значение целевой функции.
3. Значение целевой функции на каждой итерации можно рассчитать следующим образом:
F(Xk) = F(Xk-1) - γ∆ij (задача поставлена на минимум)
F(Xk) = F(Xk-1) + γ∆ij (задача поставлена на максимум)
Где γ – величина перемещаемого по циклу груза;
∆ij - оценка свободной клетки, в которую направляется груз при переходе к новому плану;
F(Xk) – значений целевой функции на k-й итерации;
F(Xk-1) – значение целевой функции на предыдущей итерации.
Рассмотрим применение метода потенциалов на примере решения сквозной задачи. Ранее был получен опорный план метода северо-западного угла.
| 304 | ||||
| 403 | 1201 | 302 | ||
| 1203 | 1307 |
План не вырожденный; F(x)=1690
Проверяем полученный план на оптимальность и находим оценки свободных клеток (согласно алгоритму)
Составляем уравнения для определения потенциалов (для каждой загруженной клетки).
α1+ β1 =4; α2+ β1 =3; α2+ β2 =1; α2+ β3 =2; α3+ β3 =3; α3+ β4 =7.
Полагая, что α3=0, то получаем: β4 =7; β3 =3; α2=-1; β2 =2; β1 =4; α1=0.
Получаем следующую таблицу.
| bj ai | αi | ||||
| 304 | α1=0 | ||||
| 403 | 1201 | 302 | α2=-1 | ||
| 1203 | 1307 | α3=0 | |||
| βj | β1 =4 | β2 =2 | β3 =3 | β4 =7 |
Далее вычисляем оценки свободных клеток и выполнения условия ∆ij< αi + βj – cij
Для клетки (1,2): 0 + 2 - 7 = -5
Для клетки (1,3): 0 + 3 - 2 = 1
Для клетки (1,4): 0 + 7 - 3 = 4
Для клетки (2,4): -1 + 7 - 4 = 2
Для клетки (1,2): 0 + 4 - 5 = -1
Для клетки (1,2): 0 + 2 - 6 = -4
Наличие положительных оценок свидетельствует о том, что план не оптимален и его можно улучшить.
Для свободной клетки, имеющей максимальную положительную оценку- +4 (клетка 1,4) строим контур (цикл) перераспределения груза, так, чтобы вершины контура лежали в загруженных клетках.
| bj ai | αi | ||||
| 30 | +43 | ||||
| -1 | |||||
| βj |
Нарисуем этот цикл. Для каждой клетки указаны ее индексы и объем поставок.
| + |
| - |
| - |
| - |
| (2.3) |
| + |
| (2.1) |
| + |
| (3.3) |
Стартовой клетке (1,4) припишем знак «+». Двигаясь по циклу, чередуем знаки. Среди поставок со знаком «-» (это клетки (1,1),(2,3),(3,4)) найдем минимальную: min(30,30,130) =30. После этого в клетках со знаком «-» уменьшим поставки на этот минимум, а в клетках со знаком «+» увеличим на этот минимум. Клетка (1,4) становится отмеченной (загруженной).
Если получена одна клетка с нулевой поставкой, то она становится пустой. У нас таких клеток две – (1,1),(2,3). Поэтому пустой объявим только одну из них с наибольшим тарифом– клетку (1,1). В клетку (2,3) будет сделана нулевая поставка, и она останется отмеченной. Это делается для выполнения соотношения: число отмеченных клеток = число столбцов + число строк – 1. Получаем новый план поставок.
| bj ai | Αi | ||||
| -4 | |||||
| 0 | +2 4 | -1 | |||
| Βj |
Для нового плана находим оценки строк и столбцов. Затем получим матрицу оценок клеток:.
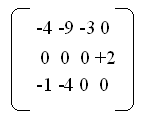
План является неоптимальным, так как оценка клетки (2,4) больше нуля. Строим для нее цикл пересчета: (2,4) – (3,4) – (3,3) – (2,3) – (2,4) и получаем новый план:
| Bj Ai | ai | ||||
| -4 | |||||
| 70 | -3 | ||||
| +1 5 | |||||
| bj |
Для нового плана находим оценки строк и столбцов. Затем получаем матрицу оценок клеток:.
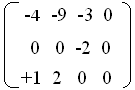
План является неоптимальным, так как оценка клетки (3,1) больше нуля. Строим для нее цикл пересчета: (3,1) - (2,1) - (2,4) - (3,4) - (3,1).
| - |
| + |
| + |
| - |
| (2.4) |
| (3.4) |
| (3.1) |
| (2.1) |
min (70,100) = 70. В клетках с «+» поставки увеличиваются на 70, а в клетках с «-» поставки уменьшаются на 70. Клетка (2,1) становится пустой. Новый план поставок:
| Bj Ai | ai | ||||
| -4 | |||||
| -3 | |||||
| bj |
Находим оценки срок и столбцов. Получаем матрицу оценок:
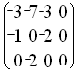
Матрица оценок не содержит положительных чисел. Получен оптимальный план поставок. Суммарные затраты на перевозку груза равны: 3*30+1*120+4*70+5*70+3*150+7*30=1500.
Напомним, что суммарные затраты на перевозку груза для первоначального плана были 1690.
Поставщик А1 должен поставить 30 единиц груза потребителю В4. Поставщик А2 должен поставить 120 единиц груза потребителю В2 и 70 единиц груза потребителю В4.. Поставщик А3 должен поставить 70 единиц груза потребителю В1, 150 единиц груза потребителю В3, 30 единиц груза потребителю В4.
Date: 2015-07-27; view: 478; Нарушение авторских прав