Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Построение экономико-математической модели задачи
|
|
Имеется m пунктов отправления (поставщиков) грузов A1, A2, A3, …, Ai, …, Am, на которых сосредоточены запасы кого-либо однородного груза в объемах соответственно a1, a2, a3, …, ai, …,am.
Величины ai определяют максимально возможные размеры вывоза груза с пунктов отправления. Суммарный запас груза поставщиков составляет 
. Кроме того, имеется n пунктов назначения B1, B2, B3, …, Bj, …, Bn, которые подали заявки на поставку грузов в объемах соответственно b1, b2, b3, …, bj, …, bn.
Суммарная величина заявок составляет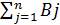 
. Стоимость перевозки одной единицы груза от поставщика Ai к потребителю Bj обозначим через cij ( транспортный тариф ), образующие матрицу транспортных издержек С. В качестве критерия оптимальности выбираем суммарные издержки по перевозке грузов.
Тогда транспортная задача формулируется следующим образом: необходимо составить оптимальный план, т.е. найти такие значения объема перевозок грузов || xij || от поставщиков Ai к потребителям Bj, чтобы вывести все грузы от поставщиков, удовлетворить заявки каждого потребителя и обеспечить минимальные транспортные расходы на перевозку груза.
Все исходные данные транспортной задачи можно записать в виде таблицы, которая называется транспортной.(табл.)
Задача заключается в определении плана перевозок – матрицы X(i=1,m; j=1,n), которая удовлетворяет следующим условиям: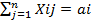 
, i=1,m, 
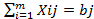, j=1,n, Xij≥0, i=1,m, j=1,n.и обеспечивает минимальное значение целевой функции 
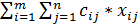min
В таком виде экономико-математическая постановка транспортной задачи считается законченной.
| Пункты отправления | Пункты назначения | Запасы ai | |||||
| B1 | B2 | … | Bj | … | Bn | ||
| A1 | c11 x11 | c12 x12 | … | c1j x1j | … | c1n x1n | a1 |
| A2 | c21 x21 | c22 x22 | … | c2j x2j | … | c2n x2n | a2 |
| … | … | … | … | … | … | … | … |
| Ai | ci1 xi1 | ci2 xi2 | … | cij xij | … | cin xin | Ai |
| … | … | … | … | … | … | … | … |
| Am | cm1 xm1 | cm2 xm2 | … | cmj xmj | … | cmn xmn | Am |
| Заявки bj | b1 | b2 | … | bj | … | bn |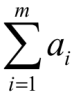 
|
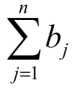
В рассмотренной модели предполагается, что суммарные запасы равны суммарным заявкам, т.е.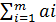 
= 
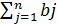. Такая задача называется закрытой транспортной задачей.
Date: 2015-07-27; view: 469; Нарушение авторских прав