Транспортная параметрическая задача

Формулировка классической транспортной задачи имеет вид:

→ min

При ограничениях:

x_ij³0

Задача формулируется следующим образом: для всех значений параметра d£l£j, где d,j - произвольные действительные числа, найти такие значения x_ij ( которые обращают в минимум функцию

=

При ограничениях:

,

x_ij³0,

Пользуясь методом потенциалов, решаем задачу приl=d до получения оптимального решения. Признаком оптимальности являются условия:

a_i+b_j – (c¢_ij+ dc²_ij)£0 для незанятых клеток,

a_i+b_j = c¢_ij+ dc²_ij для занятых клеток,

где a_i и b_j– потенциалы строк и столбцов.

Оценки представим в виде ∆_ij=μ_{ij +} lυ_ij

Значения l находятся в пределах l₁£l£l₂:

max 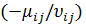если существует хотя бы одно <0,

l₁=

¥, если все ≥0.

min 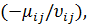если существует хотя бы одно >0,

l₂=

¥, если все £0.

Алгоритм решения задачи:

1. Задачу решаем при конкретном значении параметра l=d до получения оптимального решения.

2. Определяем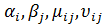

Date: 2015-07-27; view: 606; Нарушение авторских прав