
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Вычисляем значения параметра l
|
|
4. Если l<j, производим перераспределение поставок и получаем новое оптимальное решение. Если l=j, то процесс решения окончен.
Рассмотрим решение транспортной параметрической задачи на конкретном примере.
Пример 14. Имеются три поставщика однородного товара с объемами поставок: а1=100т, а2= 200т, а3=100т, и четыре потребителя с объемами потребления b1=80т,b2=120т,b3=150т,b4=50т. Стоимость транспортных расходов изменяется в определенном диапазоне в зависимости от загрузки дороги, и задана матрицей
от 5 до 11 от 4 до 1 8 от 3 до 6
4 7 от 4 до 10 от 7 до 4
5 3 6 от 1 до 10
Определить оптимальное решение перевозок, обеспечивающее минимальные транспортные затраты.
Решение. В матрицу расходов введем параметр l, где 0£l£3. Получим
5+2l 4-l 8 3+l
4 7 4+2l 7-l
5 3 6 1+3l
Полагая l=0, решаем задачу методом потенциалов, определим оптимальное решение перевозок. Распределительная таблица этого решения будет иметь следующий вид.
| bj ai | ai | ||||
| 5+2l | 4-l | 3+l | |||
| 4+2l | 7-l | -1-2l | |||
| 1+3l | -1+l | ||||
| bj | 5+2l | 4-l | 5+4l | 2+2l |
В таблице ai и bj потенциалы строк и столбцов. Для занятых клеток они определяются из условия
ai+bj = c¢ij+ dc²ij
Полагая:
a1+b1=5+2la1=0 a1=0
a1+b2=4-la2=-1-2l a2=-1-2l
a2+b1=4 a3=-1+l
a2+b3=4+2lb1= 5+2l b1=5+2l
a3+b2=3 b2= 4-l
a3+b4=1+3lb3=5+4l b3=5+4l
b4=2+2l b4=2+2l
Оценки свободных клеток находим по формуле
Dij=ai+bj – (c¢ij+ dc²ij)= 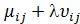
D13=a1+b3 – c¢13=5+4l+0-8= -3+4l,
D14=a1+b4 – (c¢14+lc²14)=2+2l+0-3-l= -1+l,
D22=a2+b2 – c¢22 = -1-2l+4-l-7= -4-3l.
Аналогично находим, что D24=-6+l, D31=-1+3l, D33=-2+5l.
Решение, полученное при l=0, является оптимальным для всех значений параметра l, удовлетворяющих условию
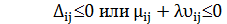
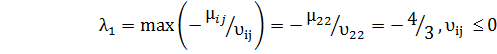
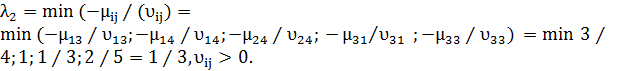
Так как по условию задачи l³0,то оптимальное решение сохраняется при 0£l£1/3. При этом минимальная стоимость транспортных расходов составляет
F(x)min=30(5+2l)+70(4-l)+50*4+150(4+2l)+50*3+50(1+2l)=1430+440l
Таким образом, при lÎ[0;1/3], F(x1)min=1430+440l и
30 70 0 0
Хопт1= 50 0 150 0
0 50 0 50
Чтобы получить оптимальное решение при l³1/3, перераспределим поставки товаров в клетку (3,1), где l2=1/3. Вновь полученное распределение представлено в таблице.
| bj ai | ui | ||||
| 5+2l | 4-l | 3+l | |||
| 4+2l | 7-l | -2+l | |||
| 1+3l | -1+l | ||||
| uj | 6-l | 4-l | 6+l | 2+2l |
Находим оценки свободных клеток:
D11=1-3l, D13= -2+l,
D14= -1+l, D22= -5,
D24= -7+4l, D33= -1+2l.
Определим пределы изменения l:

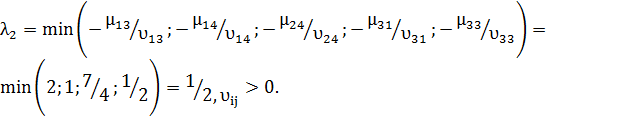
Полученное в таблице оптимальное решение сохраняется при 1/3£l£1/2. При этом F(x2)min=1460+350l.
0 100 0 0
Хопт2= 50 0 150 0
30 20 0 50
Перераспределим поставки грузов в клетку (3,3), где l2=1/2. Получим новое распределение:
| bj ai | ui | ||||
| 5+2l | 4-l | 3+l | |||
| 4+2l | 7-l | -3+3l | |||
| 1+3l | -1+l | ||||
| uj | 7-3l | 4-l | 7-l | 2+2l |
Находим оценки свободных клеток:
D11=2-5l, D13= -1-l,
D14= -1+l, D22= -6+2l,
D24= -8+6l, D33= -1-2l.
Определим пределы изменения l:
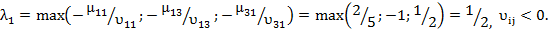
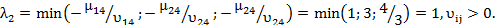
Оптимальное решение сохраняется при 1/2£l£1. При этом F(x3)min=1490+290l.
0 100 0 0
Хопт3= 80 0 120 0
0 20 30 50
Перераспределим поставки товаров в клетку (1,4), где l2=1.
| bj ai | ui | ||||
| 5+2l | 4-l | 3+l | |||
| 4+2l | 7-l | -3+3l | |||
| 1+3l | -1+l | ||||
| uj | 7-3l | 4-l | 7-l | 3+l |
Оценки свободных клеток:
D11=-1-2l, D13= -1-l,
D22= -6+2l, D24= -7+5l,
D31= 1-2l, D34= -1-l.
Пределы изменения l:
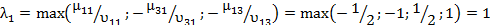
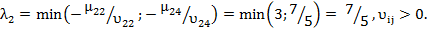
Полученное в предыдущей таблице оптимальное решение сохраняется при 1£l£7/5. При этом F(x4)min=1540+240l.
0 50 0 50
Хопт4= 80 0 120 0
0 70 30 0
Перераспределим поставки грузов в клетку (2,4), где l2=7/5.
| bj ai | ui | ||||
| 5+2l | 4-l | 3+l | |||
| 4+2l | 7-l | -3+3l | |||
| 1+3l | -1+l | ||||
| uj | 7-3l | 4-l | 7-l | 10-4l |
Оценки свободных клеток:
D11=2-5l, D13= -1-l,
D14= 7-5l, D22= -6+2l,
D31= 1-2l, D34= -8-6l.
Пределы изменения l:
l1 =max (2/5;-1;7/5;1/2;-8/6)=7/5,bij<0;
l2=min (3)=3,bij>0.
Оптимальное решение сохраняется при 7/5£l£3. При этом F(x5)min=1890-10l.
0 100 0 0
Хопт5= 80 0 70 50
0 20 80 0
Варианты контрольной работы по теме «Параметрическая транспортная задача»
Имеются три поставщика однородного товара с объектами поставок: а1=100 т., а2=200 т., а3=100 т. И четыре потребителя с объектами потребления b1=80 т., b2=120 т., b3=150 т., b4=50 т. Стоимость транспортных расходов изменяется в определенном диапазоне в зависимости от загрузки дороги, и задана матрицей
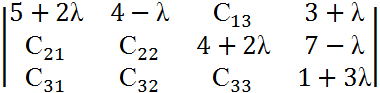
| 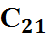
| 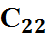
| 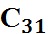
| 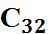
| 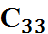
| |
Определить оптимальное решение, обеспечивающее минимальные транспортные затраты.
Date: 2015-07-27; view: 536; Нарушение авторских прав