Решение задачи методом потенциалов

Существует две группы методов получения оптимального плана транспортной задачи.

Одна группа этих методов основана на принципе последовательного улучшения плана, когда выбранный определенным образом первоначальный план при помощи расчетов улучшается до тех пор, пока он не станет оптимальным. Другая группа основана на методе последовательного сокращения невязок. Одним из методов первой группы является метод потенциалов, который основан на теории двойственности.

Для транспортной задачи (ТЗ), как и для любой ЗЛП, существует двойственная к ней задача.

Исходная задача:

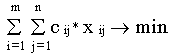
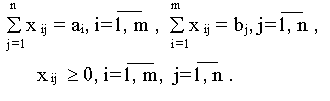
Двойственная задача:

План Х=(хij) транспортной задачи будет являться оптимальным, если существует система m+n чисел αi, βj, называемых потенциалами, удовлетворяющих условиям:

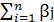max ( ai + bj)

αi + βj = cij для занятых клеток, где xij> 0, i=1,m

αi + βj ≤ cij для незанятых клеток, где xij = 0. j=1,n

Потенциалы α_i и β_j являются переменными двойственной транспортной задачи и обозначают оплату за перевозку единицы груза в пунктах отправления (поставщиками) и назначения (потребителями) соответственно, поэтому их сумма равна транспортному тарифу α_i + β_j = c_ij.

Введем обозначение оценки свободной клетки таблицы

∆_ij = α_i+ β_j – c_ij.

Если среди оценок ∆_ij нет положительных (задача поставлена на минимум), то опорный план является минимальным.

Алгоритм оценки оптимальности плана методом потенциалов включает следующие этапы.

· Построение первого опорного плана.

· Проверка вырожденности плана. Потенциалы α_i и β_j могут быть рассчитаны только для невырожденного плана.

· Определение значения функции цели путем суммирования произведений тарифов (удельных затрат) на объем производимого груза по всем занятым клеткам таблицы

· Проверка условий оптимальности. Определяем потенциалы αi и βj. Для каждой занятой клетки таблицы записываем уравнение α_i + β_j = c_ij(i=1,m; j=1,n). Получим систему (m+n-1) уравнений с (m+n) переменными.

Так как число переменных больше числа уравнений (m+n>m+n-1), то система является неопределенной и имеет бесконечное число решений. Поэтому одному из неизвестных потенциалов αi, βj задают произвольное значение, например, для одного из столбцов (отправителей)принимают потенциал αi равный нулю. При этом целесообразно нулю приравнивать потенциал того столбца, в котором имеется загруженная клетка с наибольшим тарифом. Остальные потенциалы определяют по загруженным клеткам.

Определяем оценки свободных клеток ∆_ij.

Если ∆_ij ≤ 0 (задача решается на минимум целевой функции) либо все ∆_ij ≥ 0 (задача решается на максимум целевой функции), то оптимальный план найден. Если хотя бы одна оценка свободной клетки ∆_ij> 0 (задача поставлена на минимум) или ∆_i< 0 (задача поставлена на максимум), план не является оптимальным, его можно улучшить, осуществив перераспределение груза.

· Построение нового опорного плана. Из всех положительных оценок свободных клеток выбираем наибольшую (если задача построена на минимум), из отрицательных – наибольшую по отрицательной величине (если задача построена на максимум). Клетку, которой соответствует наибольшая оценка, следует заполнить, т.е. направить груз. Заполняя выбранную клетку необходимо измерить объемы поставок, записанных в ряде других занятых и связанных с заполняемой так называемым циклом.

Циклом, или прямоугольным контуром, в таблице условий транспортной задачи называется ломана линия, вершины которой расположены в занятых клетках таблицы, а звенья –вдоль строк и столбцов, причем в каждой вершине цикла встречаются ровно два звена, одно из которых находится в строке, другое- в столбце. Если ломаная линия, образующая цикл, пересекается, то точки пересечения не являются вершинами. Для каждой свободной клетки таблицы можно построить единственный цикл.

Вершинам цикла, начиная от вершины, находящейся в свободной клетке, присваиваем поочередно знаки «+» и «-».

Из объемов груза, стоящих в минусовых клетках, выбираем наименьшее и обозначим его γ. Перераспределяем величину γ по циклу, прибавляя γ к соответствующим объемам груза, стоящим в плюсовых полюсах клеток, и вычитая γ из объемов груза, находящихся в минусовых клетках таблицы. В результате клетка, которая ранее была свободной, становится занятой, а одна из занятых клеток цикла становится свободной.

Полученный новый опорный план проверяется на оптимальность, т.е. возвращаемся к четвертому этапу алгоритма.

Date: 2015-07-27; view: 504; Нарушение авторских прав