Решение двойственной задачи

Составим и найдем решение двойственной задаче к задаче, решенной графическим и симплекс-методом.

Прямая задача:

Найти 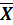=(x₁, x₂), чтобы

F(x) =16x₁+14x₂→max, при

0,8x₁+0,5x₂≤400

0,4x₁+0,8x₂≤365

x₁ - x₂≤100

X₂≤350

x₁, x₂ ≥0

Решение прямой задачи:

x₁ =312,5кг; x₂=300кг

F(x) =9200 руб.

При этом первое и втрое ограничение превращается в строгое равенство, а третье и четвертое в строгое неравенство.

Двойственная задача:

Найти 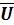=(u₁,u₂,u₃,u₄), чтобы

Z (u) = 400u₁+365u₂+100u₃+350u₄→min

при 0,8u₁+0,4u₂+u₃+0u₄≥16

0,5u₁+0,8u₂-u₃+u₄≥14

u₁ - u₄≥0

Относительно рассматриваемого варианта задач соответствующие условия “дополняющей нежесткости” первой и второй группы выглядит следующим образом.

u₁↔(400-0,8x₁-0,5x₂)=0;

u₂↔(365-0,4x₁-0,8x₂)=0; (3.12)

u₃↔(100 - x₁ - x₂)= 0;

u₄↔(350 - x₂)=0.

x₁↔ (0,8u₁+0,4u₂+ u₃ -16)=0; (3.13)

x₂↔ (0,5u₁+0,8u₂-u₃+u₄-14)=0;

Из группы условий (3.12), так как 100-312,5+300=87,5>0 и 350-300=50>0 и на основе интерпретации 1б следует, что ограничения по спросу не лимитируют оптимальную программу, т.е. u₃=u₄=0

Из группы условий (3.13) на основе интерпретации 2а следует, что если оба продукта выпускаются по оптимальной программе, т.е. x*₁=312,5 и x*₂=300, то должны выполняться равенства

0,8u₁+0,4u₂+u₃=16

0,5u₁+0,8u₂-u₃+u₄=14

Из этих уравнений с учетом u₃=u₄=0 перейдем к решению следующей системы

0,8u₁+0,4u₂=16

0,5u₁+0,8u₂=14

Откуда получаем u ₁= 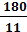(16,36) руб. и u₂= 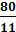(7,27) руб., при этом

Z (u) =400 · 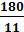+365· 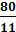=9200 руб. т. е F (x) = Z (u) =9200 руб.

В соответствие с вышесказанным найденное оптимальное решение позволяет уточнить понятие «теневая цена» это не просто цена, по которой мы будем продавать единицу того или иного ресурса. «Теневая цена» - это величина увеличения максимума целевой функции прямой задачи при изменении (увеличение) количества соответствующего ресурса на единицу, т.е.:

u₁=16,36 - величина ожидаемого прироста максимума дохода (9200 руб.) от дополнительного вовлечения в производство 1 кг молока к имеющимся 400кг;

u₂=7,27 руб.- величина ожидаемого прироста максимума дохода (9200 руб.) от дополнительного вовлечения в производство 1кг наполнителя к имеющимся 365 кг

u₃=u₄=0 руб. - величина ожидаемого прироста дохода за счет увеличения спроса (недефицитные) ресурсы.

В связи с этим «теневые цены» (u) в советской и российской литературе называются предельной эффективностью ресурса.

Date: 2015-07-27; view: 416; Нарушение авторских прав