
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Исследование предельной эффективности с помощью симплекс-метода
|
|
Как ранее указывалось прямая и двойственная задачи являются «взаимодвойственными». Следствием этого является то, что решая прямую задачу симплекс-методом мы параллельно получаем решение двойственной задачи.
В п. 3.6.4 двойственная задача решена графически и получено следующее оптимальное решение:
u1=16,36 руб; u2=7,27 руб; u3=u4=0
Z(u)min=9200 руб.
Теперь обратим внимание на строку целевой функции на последнем шаге симплексной таблице (см.симплексную таблицу).
Именно здесь и находится решение двойственной задачи.
Симплекс-метод также позволяет определить как нижнюю и верхнюю границу изменения ресурсов при неизменности «теневой цены», так и изменение структуры производственного процесса (т.е. как изменяется выпуск изделий и расходов ресурсов при изменение величины ресурсов и как при этом изменяется значение целевой функции).
Предельные значения (нижняя и верхняя границы) изменения каждого из ресурсов, для которых предельная эффективность остается неизменной, определяются как:
∆b-i= max - 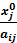 ≤ ∆ bi≤ min -
≤ ∆ bi≤ min - 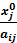 = ∆ bi+
= ∆ bi+
aij>0 aij<0
где ∆ bi – величина изменения i-го ресурса;
∆ bi - - величина уменьшения i-го ресурса;
∆ bi+ - величина увеличения i-го ресурса;
Xj0 – значение j-ой переменной в оптимальном плане;
aij - коэффициенты, структурных сдвигов для соответствующего вида ресурсов (коэффициенты столбцов базисных переменных в оптимальном плане, коэффициенты обратной матрицы к базису оптимального плана).
Проведем анализ устойчивости предельной эффективности ресурса «молоко», т.е. определим границы изменения этого ресурса, при которых предельная эффективность в 16,36 руб. остается постоянной.
Для удобства вычислений запишем рядом столбец коэффициентов структурных сдвигов по молоку и столбец оптимального решения
-0,9 300
-2,727 87,5
1,818 312,5
0,909 50
Тогда max 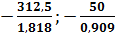
 в1≤min
в1≤min 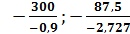
 -55 ≤△в1≤32, 1
-55 ≤△в1≤32, 1
Таким образом, ресурс «молоко» может быть уменьшен на 55 кг или увеличен на 32,1 кг. Диапазон изменения равен [ 400-55; 400+32,1]=[345; 432,1]. Верхняя граница полностью совпадает с ранее найденной.
Составим субоптимальный вариант плана с учетом изменения исходных данных.
Пусть предприятие нашло возможность увеличить запас молока на 10 кг.
| Базисные переменные | Оптимальное решение | Коэффициенты структурных сдвигов (ас) | Произведение
ac 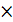 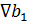 =10 =10
| Расчет варианта плана |
| X2 X5 X1 X6 | 87,5 312,5 | -0,9 -2,727 1,818 0,909 | -9 -27,27 18,18 9,09 | 60,23 330,68 59,09 |
| F (X) | u1=16,36 | 163,6 | 9363,6 |
В результате производство сливочного мороженого возросло, шоколадного - снизилось, спрос на сливочное и шоколадное мороженое тоже изменился.
Таким образом, анализ устойчивости предельной эффективности позволяет построить множество вариантов оптимальных планов с учетом изменения исходных условий задачи.
Варианты КОНТРОЛЬНЫХ РАБОТ
Предприятие осваивает выпуск 2-х новых изделий. Расходы по заработной плате, амортизационным отчислениям, материалам, лимиты, выделенные предприятию и прибыль на одно изделие приведены ниже. Решить задачу на максимум прибыли геометрически и аналитически, проанализировать полученные результаты.
| № варианта | Расход ресурсов на единицу изделия, тыс.руб. | Ресурсы материалов, выданные предприятию, тыс.руб. | Прибыль на одно изделие, тыс.руб. | ||||||||
| Изделие 1 | Изделие 2 | з/плата | амортизация | материалы | Изделие 1 | Изделие 2 | |||||
| з/плата | амортизация | материалы | з/плата | амортизация | материалы | ||||||
| 2.5 | |||||||||||
| 7.5 | |||||||||||
| 2,5 | |||||||||||
| 4.8 | 147.6 | ||||||||||
Date: 2015-07-27; view: 474; Нарушение авторских прав