
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Дифференцирование сложной функции
|
|
Теорема 1. Пусть функция 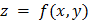 дифференцируема в точке
дифференцируема в точке 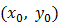 ,а ее аргументы
,а ее аргументы 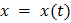 и
и 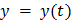 дифференцируемы в точке
дифференцируемы в точке 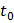 , причем
, причем 
Тогда сложная функция 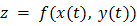 переменной
переменной 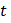 дифференцируема в точке
дифференцируема в точке 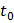 и ее производная вычисляется по формуле
и ее производная вычисляется по формуле
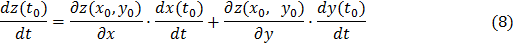
Доказательство. Так как функции 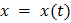 и
и 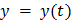 дифференцируемы в точке
дифференцируемы в точке 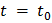 , то их приращения
, то их приращения 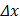 и
и 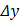 , соответствующее приращению аргумента
, соответствующее приращению аргумента 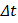 , представимы в виде:
, представимы в виде:
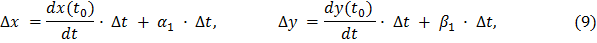
где 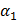 и
и 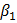 — бесконечно малые функции при
— бесконечно малые функции при 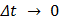 .
.
Так как функция 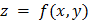 дифференцируема в точке
дифференцируема в точке 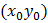 , где
, где 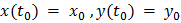 , то ее приращение
, то ее приращение 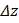 , соответствующее приращениям аргументов
, соответствующее приращениям аргументов 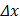 и
и 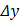 , представимо в виде
, представимо в виде
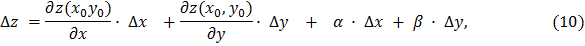
где 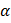 и
и 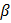 — бесконечно малые функции при
— бесконечно малые функции при  .
.
Из дифференцируемости функций 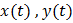 в точке
в точке 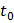 следует их непрерывность в этой точке, т.е.
следует их непрерывность в этой точке, т.е.  при
при 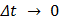 . Поэтому
. Поэтому 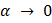 и
и 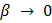 при
при 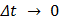 .
.
Подставляя выражения (9) в формулу (10), получаем
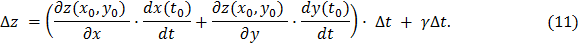
Здесь 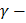 бесконечно малая функция при
бесконечно малая функция при 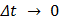 , имеющая вид:
, имеющая вид:
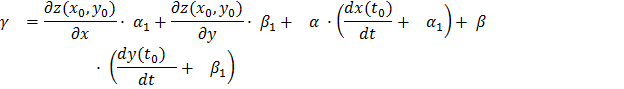
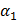 и
и 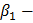 ранее показаны
ранее показаны
Обозначив в (11) выражение в скобках буквой 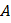 (
(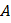 не зависит от
не зависит от 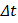 ), получаем
), получаем
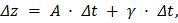
т.е. приращение 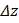 представлено как сумма линейной части приращения
представлено как сумма линейной части приращения 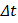 и бесконечно малой более высокого порядка, чем
и бесконечно малой более высокого порядка, чем 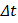 . Отсюда следуют дифференцируемость сложной функции
. Отсюда следуют дифференцируемость сложной функции 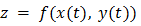 в точке
в точке 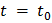 и формула (8) для
и формула (8) для 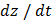 в этой точке. Теорема доказана.
в этой точке. Теорема доказана.
Аналогично формулируются и доказываются теоремы о дифференцируемости сложной функции любого числа переменных. Например:
Теорема 2. Пусть функция 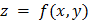 дифференцируема в точке
дифференцируема в точке 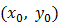 и ее аргументы
и ее аргументы 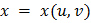 и
и 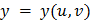 дифференцируемы в точке
дифференцируемы в точке 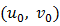 , причем
, причем 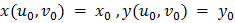 .
.
Тогда сложная функция 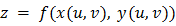 переменных
переменных 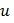 и
и 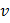 дифференцируема в точке
дифференцируема в точке 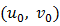 и ее частные производные вычисляются по формулам
и ее частные производные вычисляются по формулам


(Все производные в этих формулах вычисляютсявыполнены в соответствующих точках.)
Пример:
Найти частные производные функции 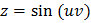 ,
,
где 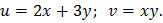 тогда в соответствии с (12 и 13) получим:
тогда в соответствии с (12 и 13) получим:
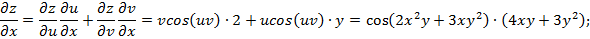
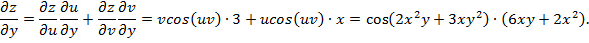
Инвариантность формы полного дифференциала
Пусть функция 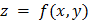 , где
, где 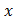 и
и 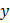 — независимые переменные, дифференцируема в некоторой точке
— независимые переменные, дифференцируема в некоторой точке 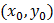 . Известно, что ее дифференциал в этой точке определяется формулой
. Известно, что ее дифференциал в этой точке определяется формулой
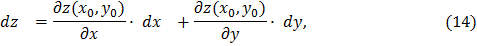
где 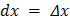 и
и 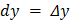 — приращения независимых переменных
— приращения независимых переменных 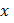 и
и 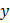 .
.
Пусть теперь 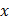 и
и 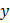 — не независимые переменные, а функции
— не независимые переменные, а функции 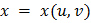 и
и 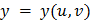 , дифференцируемые в точке
, дифференцируемые в точке 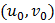 . Тогда по теореме 2 сложная функция
. Тогда по теореме 2 сложная функция 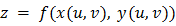 переменных
переменных 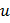 и
и 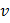 дифференцируема в точке
дифференцируема в точке 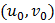 . Следовательно, ее дифференциал определяется формулой
. Следовательно, ее дифференциал определяется формулой
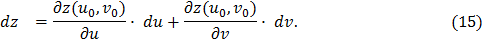
Подставляя сюда 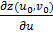 и
и 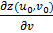 , определяемые формулами (12) и (13), и выполняя простые преобразования, получаем
, определяемые формулами (12) и (13), и выполняя простые преобразования, получаем
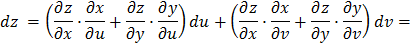
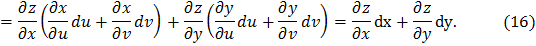
Таким образом, дифференциал функции 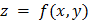 , когда
, когда 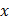 и
и 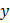 являются функциями, совпадает по форме с дифференциалом функции
являются функциями, совпадает по форме с дифференциалом функции 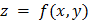 , когда
, когда 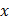 и
и 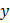 — независимые переменные. Это свойство называют инвариантностью [2] формы первого дифференциала.
— независимые переменные. Это свойство называют инвариантностью [2] формы первого дифференциала.
Следует иметь в виду, что в случае независимых переменных 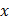 и
и 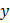 их дифференциалы
их дифференциалы 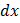 и
и 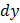 совпадают с приращениями
совпадают с приращениями 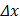 и
и 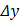 . В случае, когда
. В случае, когда 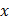 и
и 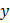 сами являются функциями, их дифференциалы, вообще говоря, не совпадают с приращениями
сами являются функциями, их дифференциалы, вообще говоря, не совпадают с приращениями 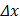 и
и 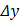 , а являются лишь их линейными частями.
, а являются лишь их линейными частями.
Свойство инвариантности формы полного дифференциала распространяется на функции любого числа переменных.
Date: 2015-07-27; view: 478; Нарушение авторских прав