Что такое энергия покоя тела?

Для понимания дальнейшего в теории движения и вихревой энергетике нэп понадобится одна очень важная формула. А именно - знаменитая формуя Эйнштейна, связывающая массу с энергией Е = mС2(c квадрат). До Эйнштейна в классическо! механике полагали, что кинетическая энергия движения тела в пространств) определяется формулой

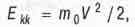(2.13)

в которой m0 - масса покоя тела, движущегося со скоростью V. Изучая фотоэффект и давление света, экспериментально открытое П. Лебедевым, А. Эйнштейн пришел к выводу, что безмассовые фотоны света несут с собой не только энергию определяемую формулой Планка но и импульс Р = Е/С. Ну а поскольку
импульс Р - это произведение массы тела на его скорость, а скорость фотонов свет: С, то в данном случае Р = mС. Отсюда следовало для фотонов:

(2.14)

То есть безмассовые фотоны при движении как бы приобретали эффективную массу тем большую, чем больше энергия фотона. Эйнштейн выдвину, предположение, что эта формула справедлива не только для фотонов, но и для любы тел. При этом масса т в данной формуле - это полная (релятивистская) масс движущегося тела, определяемая выражением (2.3). Из него следует, что покоящемуся в пространстве телу (имеющему массу покоя m0) соответствует энергия

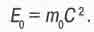(1.15)

Эйнштейн назвал ее "энергией покоя" тела, или "внутренней энергией" тела Почему внутренней? - Потому что в начале XX века люди представляли себе элементарные частицы вещества чем-то вроде сильно сжатых пружин, удерживаемых о распрямления какими-то огромными силами неизвестной природы. Энергию эти сжатых "пружин" (или прижатых друг к другу отталкивающихся электрических зарядов - составных элементов частицы) и назвали внутренней энергией вещества.
Расчеты по формуле (2.15) показывали, что в каждом грамме любого веществ содержится столько внутренней энергии, что если бы ее высвободить и превратить электроэнергию, то хватило бы на год отоплять и освещать целый город. Но в начал XX века никто не знал, как высвободить эту энергию. Лишь последующее развитии ядерной физики, физики элементарных частиц и ядерной энергетики с высоко точностью подтвердило догадку Эйнштейна и правильность формулы (2.15).
Но никто до сих пор не мог объяснить, что это за "энергия покоя" и откуда он берется. Да и строгого вывода формулы (2.15) не существовало. Сам Эйнштейн при ее выводе в [16] использовал методы приближенного исчисления, дающие заведомо не очень точные результаты. А последователи гения, угадавшего эту формулу, по примеру В. Паули пытались найти точный вывод ее с помощью интегрального исчисления. В некоторых справочниках (например, в [17]) до сих пор фигурирую этот "вывод":

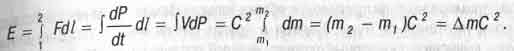(2.16)

За математической безукоризненностью этих формул составители справочников проглядели один физический "прокол". А именно, под знаком интеграла мы видим выражение 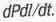. Дифференциалы в нем означают пределы бесконечно малых величин ∆Р и ∆ l при ∆ t, стремящемся к нулю. Но соотношение неопределенностей квантовой механики, открытое В. Гейзенбергом пять лет спустя после публик В Паули вышеприведенного "вывода" формулы Эйнштейна, гласит, что произвел не может быть меньше величины постоянной Планка h. Значит, в (2.16] знаком интеграла 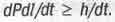. И при это выражение стремится к бесконечности вместо ожидаемой бесконечно малой величины С2(c квадрат)dm. Так квант механика зачеркнула труд разработчиков теории относительности, пользовавшихся классической механикой с ее бесконечно малыми величинами. Остается то удивляться составителям современных справочников.
Но ценность формулы Эйнштейна от этого не уменьшается, она блестяще подтверждается работой атомных электростанций, в которых высвобождает используется часть энергии покоя урана.
Современный французский критик теории относительности Л. Бриллюэн отмечал, что формулу Эйнштейна 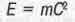"невозможно вывести ни из о, существующей в настоящее время теории или модели", как и формулу М. Планка 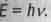. Он писал, что эти угаданные двумя гениями формулы - "не результат исходный пункт нашего мышления", что смысл "троицы", энергия = масса = час составляющей итог всех законов физики, все еще находится в глубокой тайне".
В книге [8] указан еще один возможный ответ на вопрос о том, что такое энергия покоя тела. Из закона всемирного тяготения Ньютона вытекает, что всякое тело со; вокруг себя гравитационное поле (поле тяготения), каждая точка которого характеризуется потенциалом

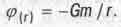(2.17)

Здесь С- постоянная тяготения, т - масса тела, г- расстояние от центра м; тела до рассматриваемой точки. Гравитационный потенциал показывает, какой энергией гравитационного взаимодействия с данным телом будет обладать в данной точке поля другое тело, имеющее массу m1.
Энергтя гравитационного взаимодействия

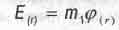(2.18)

обусловлена силами притяжения тел друг к другу. Это энергия связи тел, и ее при тать отрицательной. Например, энергия гравитационной связи с Землей яблока, лежащего на ее поверхности и имеющего массу кг, составляет -6-106(десять в шестой степени). Чтобы поднять яблоко и забросить его в дальний космос, где притяжение Земли уже изчезающе мало, надо совершить положительную работу 6-106(десять в шестой степени) Дж. Сумма этой положительной энергии и найденной выше отрицательной энергии связи и даст почти нулевую энергию связи яблока с Землей в дальнем космосе.
В этом примере мы учли притяжение яблока только к Земле. Но на него действ еще и поля тяготения от Луны, Солнца и других бесчисленных тел Вселенной Попробуем вычислить суммарный гравитационный потенциал, создаваемый всеми ими, а затем и суммарную энергию гравитационной связи нашего яблока со всеми телами Вселенной. На первый взгляд эта задача может показаться немыслимой, ибо Вселенная безгранична, а расстояния до небесных тел так велики...
Но по современным представлениям Вселенная имеет конечный объем. определяется радиусом кривизны ее пространства (или, для краткости, про радиусом Вселенной) . В этом объеме довольно равномерно распределены галактики, составляющие массу Вселенной 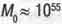г. Величины 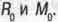хоть и не очень точно, но уже вычислены астрофизиками по результатам многочисленных наблюдений. А согласно космологическому принципу Эйнштейна все точки Вселенной равноценны. Поэтому любую из них можно рассматривать находящуюся на расстоянии R0 от "центра массы" Вселенной. Тогда гравитационный потенциал, создаваемый всей массой Вселенной в точке, где находится наше яблоко (как и в любой другой точке), будет как на поверхности шара с радиусом и массой Вселенной и составит величину

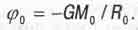(2.19)

Подставив сюда числовые значения, увидим, что 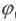0 приблизительно равен квадрату скорости света -С2(с квадрат), но со знаком минус. (Гравитационный потенциал имеет размерность квадрата скорости.)
Вычислим теперь энергию гравитационной связи тела со всеми остальные телами Вселенной как произведение массы этого тела на гравитационный потенциал Вселенной:

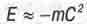(2.20)

Итак, мы неожиданно получили формулу, очень похожую на знаменитую формулу Эйнштейна для энергии покоя тела! Но формула (2.20) определяет потенциальную энергию тела в гравитационном поле Вселенной. Так это и есть "энергия покоя" тела?
Видим, что с этой точки зрения величина -С2(с квадрат) в формуле Эйнштейна - это просто квадрат скорости света, а гравитационный потенциал Вселенной.
Приблизительное, а не строгое равенство мы получили потому, что не очень то знаем величины 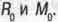. Но строгое равенство не доказано ни в одном известном выводе формулы Эйнштейна. Не исключено, что за неточностью этого равенства кроется будущая фундаментальная теория, развивающая далее теорию относительности. Ведь и казавшаяся в прошлом столь точной механика Ньютона тоже, как оказалось, давала только приблизительные значения вычисляемых величин. За этой неточностью скрывалась релятивистская механика, без которой невозможно решать такие, например, задачи, как движение частиц в ускорителях, где скорости приближаются к скорости света С.
Полученная формула (2.20) отличается от эйнштейновской еще и знаком минус потому что энергия гравитационной связи считается отрицательной. На это мои было бы сказать, что знак - дело условное, и напомнить, что на самом деле отрицательных энергий не бывает, как и отрицательных масс. Что отрицательная
энергия связи в системе из нескольких тел, например в атоме, - это всего лиш недостача положительной массы-энергии до какой-то большей величины. А в целом сумма всех энергий системы остается положительной величиной. Но в следующих разделах книги мы найдем более интересный ответ на этот вопрос об отрицательных
энергиях.
А здесь еще раз отметим, что как висящее на дереве яблоко обладает потенциальной энергией, которая высвобождается при падении яблока на земли так и все "висящие" в пространстве Вселенной тела тоже обладают такого же рода потенциальной энергией 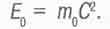. Но только они не могут "упасть" к "центру Вселенной", как не падает на планету ее спутник.

Date: 2015-07-27; view: 5768; Нарушение авторских прав