Импульс покоя тела и особые скорости движения

В разделе 1.2. предыдущей главы мы критиковали определение (1.1 "четырехскорости" Минковского, в котором действительная часть при 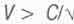2 принимала значения, большие скорости света С. Это получилось потому, что величин расстояний l и времени при этом брали из разных систем отсчета, что некорректно
Но именно так экипажам космических межзвездных кораблей в будущем удобн(всего будет выражать и измерять "собственную скорость" корабля:

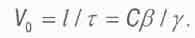(2.21)

Ведь расстояния l до той или иной звезды указаны в атласах по земным мерка? а время полета корабля г экипажу удобнее измерять по своим собственным часам "Собственная скорость" может оказаться и больше скорости света С, хотя для земного наблюдателя скорости V0 будет соответствовать скорость V = V0 у, всегда меньше скорости света С.
А вычисляя импульс своего корабля, его экипаж будет просто умножать масса покоя корабля m0 на "собственную скорость":

(2.22)

И в самом деле, не пересчитывать же каждый раз массу корабля по релятивистской формуле (2.3) зависимости массы от скорости! Для космонавта масса его корабля как и масса его собственного тела, не зависит от скорости корабля, а всего представляется ему равной массе покоя m0, которая в СТО считается инварианта
при преобразованиях Лоренца, так же, как считается инвариантным собственное время.
Получаемая по (2.22) величина импульса соответствует релятивистскому импульсу корабля, вычисляемому земным наблюдателем по формуле Р = mV, в которой m = m0/ y релятивистская масса корабля.
По аналогии с существующим в СТО выражением "энергия покоя" тела назовем величину "

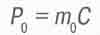(2.23)

импульсом покоя" тела. Он, конечно же, равен рассмотренному в разделе 2.1 количеству движения во времени (2.2) тела, покоящегося в пространстве и инвариант при преобразованиях Лоренца.
В формулах (2.21) и (2.22) появился любопытный сомножитель - отношение ß/y на который обращалось внимание еще в книге [8]. Это отношение озна безразмерную собственную скорость тела

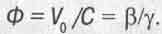(2.24)

В книге [8] была обнаружена точка перегиба на графике зависимости Ф от y. А ведь графики давно известных в СТО зависимостей релятивистского импульса Р и полной (релятивистской) энергии тела от безразмерной скорости ß движения данного тела в пространстве (см. рис. 2.1 а) не имеют особых точек. Последнее вполне соответствовало эйнштейновскому утверждению о равноправии всех скоростей движения. Эйнштейн многократно подчеркивал, что в природе нет выделенных (особых) скоростей движения, ибо это вытекало из его постулатов. И вот на графике функции Ф (у), а также на графиках V0(у) и Р(у), которые выражаются одной и той же кривой, построенной на рисунке 2.1 б, мы видим точку перегиба при 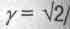3(ей соответствует скорость движения в пространстве 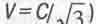. В [8] обнаружены и
перегиба на графиках еще двух функций (при 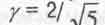и при у ~ 0.933)
наибольшую важность для нас имеет, конечно же, приведенная здесь кривая зависимости импульса тела Р от скорости у движения этого тела во времени.
Эйнштейновское утверждение о равноправии всех скоростей предполагало отсутствие особых точек на графиках зависимостей энергии и импульса тела от его скорости. Но никому не приходило в голову строить графики зависимостей величин от какого-то "фактора Лоренца", как называли величину 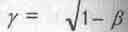2(бетта в квадрате)
догадываясь, что она означает скорость движения тела во времени.

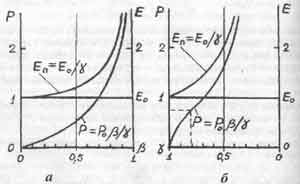
Рис. 2.1

Отмеченные выше скорости, соответствующие точкам перегиба графиков, можно назвать особыми скоростями движения. Следует согласиться, что скорость с вакууме С - тоже особая скорость, можно сказать, самая особая, мировая коне Следующая за ней по важности - особая скорость, которая в [8] названа "первой космической скоростью Вселенной" в предложении, что с такой скор движутся наиболее отдаленные от нас галактики, и что именно с такой скор движется относительно "центра масс Вселенной" каждое ее тело. При этой скорости ß = у и потому достигается равнораспределение энергий движения в пространстве и во времени и наблюдается ряд экстремумов на графиках, строившихся в [8].
Отмеченные выше скорости, соответствующие точкам перегиба графиков, можно назвать особыми скоростями движения. Следует согласиться, что скорость с вакууме С - тоже особая скорость, можно сказать, самая особая, мировая коне Следующая за ней по важности - особая скорость 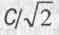, которая в [8] названа "первой космической скоростью Вселенной" в предложении, что с такой скор движутся наиболее отдаленные от нас галактики, и что именно с такой скор движется относительно "центра масс Вселенной" каждое ее тело. При этой скорости ß = у и потому достигается равнораспределение энергий движения в пространстве и во времени и наблюдается ряд экстремумов на графиках, строившихся в [8].
Называя указанные скорости движений особыми, мы, казалось бы, замахиваемся на то, что еще недавно считалось святая святых современной физики - постулаты Эйнштейна. Но ведь найденные точки перегибов и экстремумов существуют! От этого факта уже не отмахнуться, как не отмахнуться и от наличия во Вселенной выдел (абсолютной) системы отсчета, связанной с реликтовым излучением. Остается только выяснить, в каких процессах проявляются эти особые скорости.
Кстати, с особой скоростью 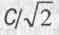мы имеем дело повседневно: т минимальная скорость распространения света (электромагнитных волн) в Случайно ли? Ведь вода хранит в себе столько тайн и обладает столь удивительными аномальными свойствами, отличающими ее от других веществ. А совпадения природе редко бывают лучайными.

Date: 2015-07-27; view: 855; Нарушение авторских прав