Основная диаграмма теории движения

Основное уравнение (1.16) теории движения является не чем иным, как каноническим уравнением плоской центральной кривой второго порядка

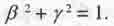
Его решения - попарные значения величин ß и у, удовлетворяющие этому уравнению. Совокупность всех возможных решений образует на комплексной плоскости (ß, iу) график уравнения (1.16).
Если ß и у - действительные числа, то графиком уравнения (1.16) является окружность, имеющая радиус, равный единице (см. рис. 1.1). Эту окружность описывает вокруг начала осей координат на комплексной плоскости конец радиуса-вектора комплексной скорости

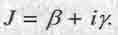
Взаимно перпендикулярными осями координат этой плоскости является действительная ось Oß безразмерной скорости движения материальной точки в пространстве (ось абсцисс) и мнимая ось Оiy безразмерной скорости движения той же точки во времени (ось ординат). Длина радиуса - вектора J, принятая за единицу, равна модулю комплексного числа J, характеризующего движение этой материальной точки в комплексном пространстве - времени нашего четырехмерного мира. Вся теория движения, изложенная выше, а подробнее в [8], вытекает из графика этой окружности.

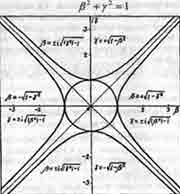
Рис. 1.1. Основная диаграмма теории движения (9).

Но до сих пор мы рассматривали только действительные значения величин ß и у А ведь существуют и мнимые числа, которые в математике имеют не меньшие права, чем действительные. Предположим, что безразмерная скорость ß движения объекта в пространстве выражается положительным или отрицательным мнимым числом. Тогда уравнение (1.16) останется справедливым, если скорость движения того же объекта во времени

(1.23)

по абсолютной величине будет больше единицы. Притом величины у будут оставаться действительными числами, принимающими положительные и отрицательные значения.
Основное уравнение (1.16) при 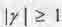и при ß -мнимом превращается в уравнение гиперболы:

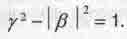(1.24)

Верхняя и нижняя ветви этой гиперболы (см. рис. 1.1) касаются единичной окружности в точках пересечения с осью ординат.
Отметим, что абсолютные величины 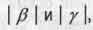удовлетворяющие уравнению (1.24), не имеют ограничений сверху. То есть они лежат в пределах

(1.25)

Отметим еще, что при мнимом ß комплексная скорость 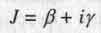становится чисто мнимой величиной.
Как видим, скорости движения ß по своей абсолютной величине здесь могут называться за пределами дозволенного теорией относительности, то есть становятся больше единицы, а скорости у вообще всегда больше единицы, если ß - мнимое число. Поэтому области на рис. 1.1, описываемые верхней и нижней ветвями гиперболы (1.24), названы в книге [9] "вертикальным запредельным миром", в отличие от допредельного мира, описываемого единичной окружностью, характеризующей поступательное движение обычных тел с досветовыми скоростями.
Предположим теперь, что мнимым числом является величина безразмерной скорости у движения объекта во времени. Тогда основное уравнение (1.16) останется справедливым, если величина безразмерной скорости движения этого объекта в пространстве

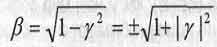(1.26)

по абсолютной величине будет больше единицы. Притом (3 будет оставаться действительным числом (положительным или отрицательным). Основное уравнение (1.16) при |ß |>= 1 и при мнимых превращается в уравнение гиперболы, сопряженной с предыдущей:

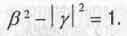(1.27)

Правая и левая ветви этой гиперболы (см. рис. 1.1) касаются единичной окружности в точках пересечения с осью абсцисс.
И опять абсолютные величины безразмерных скоростей ß и у не имеют ограничений сверху:

(1.28)

А комплексная скорость движения J= ß + iy становится чисто действительной величиной (так как мнимая ее часть iy=i(|iy|)=-|y| становится действительным числом).
Области на рис. 1.1, описываемые правой и левой ветвями гиперболы (1.27), названы в книге [9] "горизонтальным запредельным миром". В этом мире должно наблюдаться довольно странное явление. А именно, в результате того, что мнимая часть комплексной скорости J становится действительным числом, движение во времени тут становится реальным, а не мнимым! Это означает, что объект, совершающий такое движение, не может быть обнаружен ни в какой точке времени, так как непрерывно перемещается сквозь "пласты времени", как бы пересекая их. Если в данный момент (по нашим часам) он в течение какого-то мгновения, продолжительность которого определяется, по-видимому, соотношением неопределенностей квантовой механики, присутствует в нашем мире вместе с нами, то в следующий миг он уже во вчерашнем или в завтрашнем нашем дне, в то время как мы остались в сегодняшнем и медленно движемся в завтрашний вместе с окружающими нас реальными предметами нашего мира досветовых скоростей. В результате этот объект, который можно назвать виртуальным, сегодня для нас уже недосягаем и неуловим. В книге [9] показано, что правая и левая полуветви основной диаграммы теории движения описывают движение гипотетических сверхсветовых частиц - тахионов, теорию которых физики начали разрабатывать еще в 60-е годы [15]. Но экспериментаторам несмотря на многочисленные попытки, до сих пор не удалось зарегистрировать тахионы, по-видимому в силу вышеуказанной их особенности движения во времени, делающей тахионы почти ненаблюдаемыми.
Понимание этой особенности, дающееся теорией движения, может теперь позволить экспериментаторам по-иному взглянуть на проблемы регистрации тахионо Более того, теория движения, дающая новый мощный толчок развитию теории там онов, указывает, что виртуальные частицы в квантовой теории поля - это тахиож что неуловимые гравитоны - это тоже тахионы, а потому гравитация распространяв ся со скоростями, на много порядков величины превосходящими скорость света вакууме. Более того, в книге [9] показано, что всепроникающие нейтрино - это, по видимому, тоже тахионы! А нейтрино уже зарегистрированы экспериментально. Значит, тахионы все-таки можно регистрировать?
Теория движения показывает, что виртуальный мир сверхсветовых частиц должен быть столь же богат (если не богаче), как и наш мир досветовых частиц. Богаче с может быть хотя бы потому, что тахионы обладают способностью двигаться во врем< ни как вперед, так и назад (а мы - только вперед). В [9] развивается гипотеза укр< инского физика из г. Бердянска М. Т. Попова о том, что именно тахионы нес] информацию из будущего, которую каким-то образом воспринимают ясновидцы гадалки.
В заключение данной главы отметим следующее. Если движение объектов в "горизонтальном запредельном мире" описывается чисто действительной скоростью, а движение объектов "вертикального запредельного мира" - чисто мнимой J, то читатели могут подумать, что объекты "вертикального запредельного мира" обнаружить еще сложнее, чем "горизонтального". Но четвертая глава покажет, что наоборот. Более того, читатели увидят, что с объектами "вертикального запредельного мирг они имеют дело буквально на каждом шагу и хорошо с ними знакомы. Только вс достаточно ли хорошо?

Date: 2015-07-27; view: 698; Нарушение авторских прав