Основные ошибки и упущения СТО

В теории относительности огромную роль играет представление о четырехмерном пространстве-времени и об интервале как расстоянии между точками в нем. В доэйнштейновские времена полагали, что пространство Вселенной трехмерно и описывается эвклидовой геометрией с декартовыми осями координат х, у, г. Но когда описывают движение тела, например, когда чертят график движения поезда, то вдоль одной оси координат на листе бумаги откладывают расстояния, а вдоль другой - время t. Ось времени - четвертая ось координат - еще с догалилеевских времен неявно присутствовала в описаниях движения тел, только люди не осознавали этого.
Первым осознал Г.Минковский, помогавший Эйнштейну создавать математический аппарат теории относительности. Он в 1908 г. и объединил пространство и время в единое четырехмерное пространство-время.
Поскольку движения во времени из прошлого в будущее мы не видим, а только понимаем (мним), что оно существует, Минковской назвал четвертую (временную) ось координат мнимой.
Если трехмерное пространство еще можно изобразить на листе бумаги с помощью изометрии, то четырехмерное уже невозможно. Но СТО первоначально рассматривала только прямолинейные и равномерные движения тел вдоль одной оси координат. Поэтому Минковский вслед за составителями графиков движения поездов стал откладывать на одной оси координат плоскости листа бумаги расстояния l в трехмерном пространстве, а на другой, перпендикулярной ей оси - мнимые "расстояния" во времени iСt Здесь символ 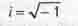означает мнимую единицу, а на скорость света в вакууме С домножено для того, чтобы "расстояния во времени" имели ту же размерность (метры), что и расстояния в пространстве.
В результате получилась комплексная плоскость (l, iСt), действительная и мнимая оси координат которой пересекаются в точке 0, принятой за начало отсчета координат. Всякая точка на такой плоскости в математике описывается комплексным числом

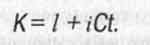(1.1)

Теория комплексных чисел к началу XX века была уже достаточно хорошо разработана математиками. Поэтому далее разработчикам СТО требовалось лишь строго следовать ей. Но они этого не сделали, а начали изобретать свою смесь теории комплексных чисел с векторной алгеброй.
В последней длинавектора, илиотрезка ∆ l, связанас длинамиего проекций (∆х, ∆у, ∆z) надекартовы осикоординат теоремой Пифагора:

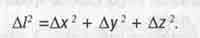(1.2)

Минковский стал вычислять расстояние ∆ l между точкамичетырехмерного пространства-временипо тому же правилу:

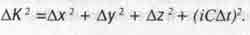(1.3)

А поскольку то данное выражение он переписал в виде:

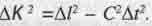(1.4)

Появившийся здесь знак минуса противоречил теореме Пифагора, требовавшей плюса. Тогда создатели СТО и сформулировали "псевдопифагорову теорему": квадрат гипотенузы 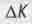равен разности квадратов катетов И хотя треугольника такими свойствами не начертить даже с помощью неэвклидовой геометрии Римана, ссылки на которую любил делать Эйнштейн, объяснили, что такова уж особенность четырехмерного пространства-времени. Эйнштейн назвал это эфемерное пространство "квазиэвклидовым" [10].
Для чего потребовалась столь смелая "модернизация" геометрии? Дело в том, что в классической механике преобразования Галилея при переходе от одной инерциальной системы отсчета координат к другой оставляли неизменным расстояния в трехмерном пространстве. Разработчикам СТО хотелось, чтобы по аналогии с этим используемые ими преобразования Лоренца, заменившие в СТС преобразования Галилея, оставляли неизменной (инвариантной) не только скорости света С (для чего они и были найдены X. Лоренцем), но и расстояние между точкам! четырехмерного пространства - времени [11]. Однако величина ∆К, вычисляемся и; формулы (1.3) оставалась инвариантной при преобразованиях Лоренца только когд; в формуле (1.4) между ее слагаемыми был знак минуса. Более того, когда и само значение 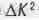брали со знаком минуса. В конце концов разработчики СТО записали:

(1.5)

Определяемую так величину ∆S назвали интервалом, понимая его какрасстояы между точками пространства-времени [12].
Казалось бы, что все вроде правильно, хотя и требовало ломки сложившихся представлений эвклидовой геометрии, принятия без доказательств "псевдопифагоровой теоремы" и отказа даже от попыток наглядно представить происходящее в "псевдоэвклидовом" пространстве. Но этот отрыв физики от наглядности скоро был объяв лен не недостатком, а достижением теории.
Благодаря своей инвариантности, облегчающей расчеты, понятие интервала как расстояния между точками "четырехмерного континуума" стало широко использоваться в СТО, а затем и в ОТО, где все зиждется на понятии об интервале. Но разберемся, насколько верно его определение.
Точку в четырехмерном пространстве-времени Минковского, называемом "миром Минковского", описываемую комплексным числом (1.1), в СТО называют "мировой точкой". При ее движении в пространстве - времени она рисует на плоскости листа бумаги "мировую линию".
Комплексная длина бесконечно малого отрезка этой линии, или дифференциал комплексного числа, в теории комплексных чисел определяется выражением [13]:

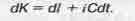(1.6)

Возведем этот дифференциал во вторую степень:

(1.7)

Мы получили новое комплексное число. В нем выражение в квадоатных скобках, являющееся действительной его частью, и есть та самая величина 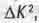которую мы видели в формуле (1.4). Поэтому можно сделать вывод, что то выражение, которое в СЮ называют квадратом дифференциала интервала dS и понимают его как квадрат бесконечно малого расстояния между точками пространства-времени, на самом деле является лишь взятой с противоположным знаком действительной частью квадрата бесконечно малого отрезка комплексной длины мировой линии.
А вот мнимая его часть 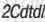ускользнула от внимания разработчиков СТО. И только в ОТО мнимая часть выражения (1.7) была учтена, хотя разработчики ОТО так и не осознали, что интервал - это отнюдь не расстояние между точками пространства-времени. Но не будем углубляться в ОТО, а вернемся к комплексной плоскости мира Минковского, точку на которой описывает комплексное число (1.1).
В теории комплексных чисел расстояние между точками 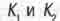комплексной плоскости вычисляют как модуль (абсолютную величину) разности 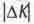комплексных чисел, описывающих данные точки. Этот модуль определяют из теоремы Пифагора:

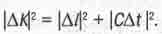(1.8)

Видим, что ошибка Минковского состояла в том, что он напрасно оставлял в выражении (1.3) символ i, а затем возводил его во вторую степень и совершенно напрасно поставил в получившемся выражении (1.4) знак минуса.
Чем же тогда на самом деле является так называемый интервал ∆S, определяемый из выражения (1.5), если это не расстояние между точками пространства-времени?
Чтобы ответить на этот вопрос, надо, оказывается, сначала внимательно разобраться в том, как определять скорость движения в пространстве-времени. В классической механике среднюю скорость V движения тела в пространстве определяют как отношение длины пути 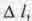пройденного телом, ко времени ∆t, за которое пройден этот путь. А мгновенную скорость V определяют как производную от l по dt (11. Если по аналогии с этим определять скорость движения точки в пространстве - времени "мира Минковского", то надо взять производную по dt от комплексного числа К, описывающего данную точку:

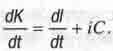(1.9)

Действительная часть здесь оказалась не чем иным, как скоростью V движения точки в пространстве, определяемой классической механикой. Это должно бы Радовать, так как соответствует принципу дополнительности. Однако мнимая временная) часть у получившегося выражения (1.9) оказалась константой С. Из этого можно было бы сделать ошибочный вывод, что всякое тело всегда движется во времени с постоянной скоростью С, которая ни от чего не зависит. Но это противоречило бы! самой же теории относительности, открывшей людям, что ход времени на движущемся теле зависит от скорости его движения в пространстве. (Несложно понять, что ход времени и скорость движения во времени - величины взаимосвязанные).
Г. Минковский нашел выход (к сожалению, как мы сейчас покажем, не наилучший) из этого затруднительного положения - стал определять скорость движения точки в пространстве-времени как производную от К по собственному времени , отсчитываемому часами, перемещающимися вместе с движущимся телом! (измеряемому его собственными часами).
Ведь Эйнштейн уже в первой своей публикации [1] 1905 г. по СТО показал, чтя движущиеся часы должны идти медленнее неподвижных, и что при движении тела ‹ t в соответствии с его формулой

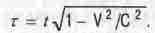(1.10)

Поэтому при дифференцировании комплексного числа (1.1) по мнимая часта получающегося выражения уже не была константой. Определяемую так скорость; движения точки в пространстве-времени своего "мира" Минковский назвал "четырехскоростью":

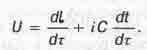(1.11)

Он отмечал, что достоинством такого определения является то, что дифференцирование осуществляется по величине d , которая инвариантна при преобразованиях Лоренца, что облегчало расчеты.
Физики и по сей день пользуются таким определением четырехскорости, записывая его, правда, в несколько ином виде:

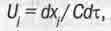(1.12)

который делает четьюехскорость безразмерной величиной (здесь j=1, 2, 3, 4;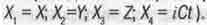
Но обратим внимание на то, что мнимая (временная) часть четырехскорости в выражении (1.11) при V > О больше скорости света С и устремляется к бесконечности, когда V —›С. Да и действительная часть четырехскорости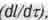
возрастая с ростом скорости V, становится больше скорости света С, когда V превышает величину 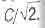Это как-то не очень вяжется с постулатом Эйнштейна, провозглашающим, что в природе не существует скоростей движений тел, больших скорости света в вакууме С. Разработчикам СТО не удалось найти выхода из этой щекотливой ситуации, и тогда четырехскорость (1.11) и была преобразована в безразмерную величину (1.12) чтобы хоть как-то завуалировать указанное противоречие.
А ведь оно возникает лишь от того, что величины l и взяты из разных систем отсчета: l - из неподвижной, связанной с наблюдателем, относительно которого происходит движение, - из движущейся, связанной с перемещающимся телом. Так определять скорость движения тела некорректно!

Date: 2015-07-27; view: 782; Нарушение авторских прав