Что такое интервал и новое определение осей координат четырехмерного пространства-времени, возвращающее его к эвклидовой геометрии

Вернемся к вопросу о том, что такое интервал. Приняв новое определение "пути во времени" т, мы должны заменить на комплексной плоскости "мира Минковского" ось OlCt осью OlC . Всякая точка на такой новой комплексной плоскости теперь будет описываться комплексным числом

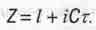(1.18)

Его можно получить и другим путем: домножив на С обе части выражения (1.17) и проинтегрировав их по dt.
Непривычной и необычной, на первый взгляд, получается наша новая комплексная плоскость, одна координата (l) на которой определяется измерениями одного наблюдателя, а другая (Сг) - другого, движущегося относительно первого. Но ведь это комплексная плоскость расстояний. Ее ось Ol - это ось расстояний в пространстве, которые проходит тело за время t, отсчитываемое часами неподвижного наблюдателя, другая же ее ось OiC - это ось "расстояний" С во времени, которые проходит то же тело за то же время t, отсчитываемое часами того же наблюдателя, относительно которого движется данное тело.
Определим теперь квадрат расстояния между точками 0 и Z нашей комплексной плоскости (l, iC ) как квадрат модуля комплексного числа

(1.19)

Если подставить сюда значения l = ßCt и - уt, то с учетом уравнения (1.16) получим:

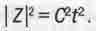(1.20)

Это значит, что расстояние от начала осей координат до точки Z нашего четырехмерного "мира" равно Сt. Полученный результат отражает тот уже отмечавшийся выше факт, что все тела в нашем комплексном ространстве-времени движутся с одной и той же по абсолютной величине комплексной скоростью J, имеющей модуль |С|.
А вот если подставить полученное значение 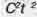вместо 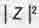в (1.19), будем иметь:

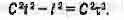(1.21)

Левая часть этого уравнения есть не что иное, как известное и бывшее столь загадочным выражение (1.5) для квадрата интервала. Значит, интервал 5 - это "расстояние" Ст, которое проходит тело во времени за время t, выраженное благодаря коэффициенту С в тех же единицах длины (метрах), что и расстояние I, проходимое этим телом в пространстве за то же время т., отсчитанное наблюдателем, относительно которого движется данное тело.
Впрочем, формулу dS = Cd нам и доказывать не надо, она давно известна в СТО [14].
С учетом этого запишем окончательное выражение для квадрата расстояния ∆ 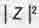между точками нашего комплексного пространства-времени:

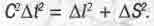(1.22)

Как видите, это расстояние определяется теоремой Пифагора. А еще видим, что это фактически то же самое выражение, что и эйнштейновское (1.5) для квадрата интервала. Только теперь оно записано в нормальном виде: квадрат гипотенузы С∆t равен сумме квадратов катетов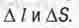
Эвклидова геометрия восторжествовала! И уже не нужны ни "псевдопифагорова теорема", ни "квазиэвклидовое пространство", бывшие, как мы теперь понимаем, вынужденными уловками разработчиков СТО на неосознанном ими пути к уравнению (1.22), задаваемому самой Природой.

Date: 2015-07-27; view: 707; Нарушение авторских прав