Глава третья энергия в теории движения

3.1. Что такое энергия движения во времени?

Условившись применять по мере возможности законы обычной механики к движению тел во времени, подумаем теперь над тем, может ли существовать энергия движения тела во времени Ет. Мы уже поняли, что покоящееся в пространстве тело движется во времени с наибольшей мнимой скоростью у0= 1. Следовательно, оно в состоянии покоя будет обладать максимальной энергией движения во времени если последняя существует. Интересно, как будет соотноситься эта энергия с энергией покоя тела Е0? А с полной энергией тела Еп?
В СТО полная энергия движущегося тела определяется формулой Эйнштейна Еп= mС2(с квадрат). Подставляя сюда значения m из (2.3) и учитывая (2.15), получают

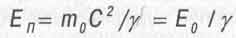(3.1)

где, напомним,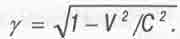
В учебниках часто приводят график зависимости 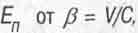который мы воспроизводим на рисунке 3.1. Справедливо полагают, что полная энергия складывается из энергии покоя тела E0 = m0C2(с квадрат) и кинетической энергии Ек, которую тело получает от движения, ускоряющего данное тело до скорости V. То есть

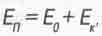(3.2)

Исходя из этого, в СТО кинетическую энергию Ек определяют как разность

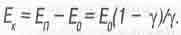(3.3)

Кривая ее графика в точности повторяет кривую для Еn только проходит ниже на величину Е0 (см. рис. 3.1).

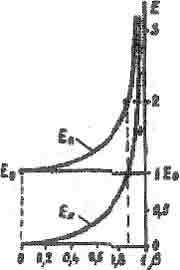Рис (3.1)

Эти графики обычно не привлекают внимание исследователей. Но из них следует интересный для нас вывод о том, что кинетическая энергия и энергия покоя тела суммируются аддитивно как скалярные величины. Это соответствует классической механике, которой разлагают скорость тела на компоненты, находят энергию ее движения вдоль каждой из них, а затем складывают вычисленные компоненты энергии как скаляры. Попробуем применить это правило и для вычисления энергии движения тела во времени.
Но сначала определим точнее это понятие. Для этого умножим обе части уравнения (1.16) на
Еп=mС2 (с квадрат).Получим:

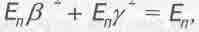(3.4)

Назовем компоненту

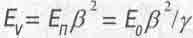(3.5)

энергией движения тела в пространстве, а компоненту

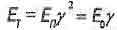(3.6)

энергией движения тела во времени.
На рисунке 3.2 приведены графики этих энергий как функции от скоро движения тела во времени у, величина которой отложена на оси абсцисс в линейном масштабе, а величина ß - в нелинейном (на рис. 3.1. в линейном масштабе вкладывали, наоборот, величину ß). Надо сказать, что при переходе от линейной к нелинейной шкале оси абсцисс картина хода кривых изменяется, хотя все координ их точек остаются теми же.

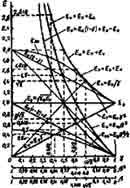Рис.(3.2)

График зависимости Еп от у (рис. 3.2) представляет собой гиперболу а зависимость Eт от у - наклонную прямую, что соответствует линейному уравнению (3.6).
Видим, что с уменьшением скорости движения тела во времени энергия его движения во времен уменьшается линейно. При этом покоящемуся в пространстве телу соответствует Ет = E0, Ev = 0. Значит энергия покоя тела Е0 - это энергия движения во времени тeла покоящегося в пространстве.
Поколения физиков лом головы над вопросом, что такое таинственная "энергия покоя" тела, понятие о которой ввел Эйнштейн не расшифровав это понятие. И мы с вами наконец выяснили, что такое. Вы спросите, что тогда такое потенциальная энергия тела в гpавитационном поле Вселенной которой велась речь в предыдущем разделе? Но ничто не запрещает, чтобы это была одна и та же энергия.
Дуализм!
Рассматривая рис. 3.2, замечаем, что если энергия движения тела в пространстве может расти неограниченно с увеличением ß то энергия его движения во времени не превышает величину Е0. Но поначалу, при 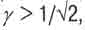, она больше энергии движения в пространстве. Такое поведение энергии определяется неукоснительным соблюдением закона сохранения количества движения тела во времени, о котором мы говорили в разделе 2.1.
Может, скорость движения 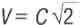потому и является особой скоростью, что при ней достигается не только равенство скоростей движения тела в пространстве и во времени y, но и равенство энергий этих движений. То есть достигается равнораспределение энергий движения в пространстве и во времени.

3.2. Можно ли использовать энергию движения во времени?

Эйнштейн, показав, что энергия покоя тела Е0 инвариантна при преобразованиях Лоренца, отождествлял ее с внутренней энергией этого тела. Мы же всё более убеждаемся, что эти два термина обозначают разные понятия, что под внутренней энергией тела следует понимать энергию движения данного тела во времени Ет, которая уменьшается с ростом скорости V движения тела, а потому далеко не инвариантна, в отличие от Е0.
Хотя с увеличением скорости V движения тела в пространстве энергия его движения во времени Ет уменьшается, полная (релятивистская) энергия Еп этого тела растет в соответствии с (3.1). Следовательно, при замедлении движения тела во времени разность энергий

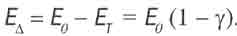(3.7)

превращается в часть энергии движения тела в пространстве и суммируется с кинетической энергией Ек, привносимой движителем. Вместе они и составляют энергию движения тела в пространстве:

(3.8)

Другими словами, часть массы-энергии покоя тела Е0 превращается в энергию его движения в пространстве Ev Ну а в сумме энергии ЕVи Ет составляют полную (релятивистскую) энергию тела

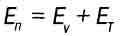(3.9)

Но поскольку масса и энергия - понятия эквивалентные, то эти превращения энергии из одного вида в другой для наблюдателя остаются незамеченными. Для нeгo имеет значение лишь полная (релятивистская) масса-энергия тела Eп, которая проявляет себя и как инертная, и как гравитационная масса данного тела. Некоторые просят, стоит ли тогда писать все эти формулы с энергией движения во времени, если в результате она никак себя не обнаруживает? Но можно надеяться (и, как будет показано в следующей главе, не без оснований), что существуют такие процессы, на которые движение в пространстве и движение во времени сказываются по-разному.
Если при замедлении движения тела во времени часть энергии этого мнимого движения превращается в энергию движения в пространстве, то возникает вопрос: а нельзя ли найти такие условия, при которых эту энергию, бывшую до того частью "энергии покоя" тела, можно было бы использовать в полезных целях, например высвечивая ее в виде излучения, а затем превращая в электроэнергию. Ведь это огромная энергия! Из каждого грамма вещества - "топлива" - ее могло бы выделяться в тысячи раз больше, чем выделяется из грамма урана в ядерном реакторе. Это было бы самое калорийное "топливо"! В таком процессе масса непосредственно превращалась бы в энергию, а "топливом" могло бы служить любое вещество.
Ведь атомы любого вещества - это словно консервы со сгустками энергии. Но туристы хорошо знают, что можно умереть от голода на мешке с запаянными консервными банками, если не иметь ключа для их открывания. Таковым "ключом" для высвобождения внутренней энергии вещества до последнего времени считались только ядерные реакции, протекающие, например, в реакторах атомных электростанций и в атомной и водородной бомбах. Но и там для эффективного протекания процесса требуется создавать особые условия (критические массы, сверхвысокие температуры). Да и опасны эти источники энергии. А потому дорогие и в конечном счете низкоэффективные. Поэтому надо продолжать поиски других "ключей" для высвобождения внутренней энергии вещества.
Из вышеизложенного понятно, что для высвобождения внутренней энергии вещества необходимо прежде всего замедлять движение его во времени, ускоряя движение в пространстве. А для этого необходимо привносить извне кинетическую энергию, притом большую той, которая выделяется. Процесс на первый взгляд может показаться энергетически невыгодным. Но только на первый взгляд. Ведь и для получения энергии от сжигания угля необходимо сперва разогреть уголь до воспламенения. Вложенная извне энергия не исчезает, а остается в системе, при этом выделяющаяся энергия, которую мы хотели бы использовать, добавляется к ней. Посмотрите: кривая графика для Еv на рис. 3.2 лежит выше кривой Eк. Расстояние между ними и есть выигрыш в энергии. Он появляется уже при значениях у, близких к 1. Это значит, что не до такой уж большой температуры надо разогревать наше "топливо", чтобы получить ощутимый выход энергии. Может, даже температуры топки паровоза хватило бы, чтобы разогнать молекулы "топлива" до необходимых скоростей теплового движения?
Конечно, для этого надо знать, в каком именно веществе наиболее легко может пойти такой процесс высвечивания внутренней энергии, и надо знать, при каких условиях он может идти наиболее эффективно. Ведь и обыкновенный уголь в обыкновенной топке не при любых условиях загорается.
И только ли ускорением в пространстве можно тормозить движение тела во времени? Может, существуют более рациональные методы? Ведь мы только-только осваиваем азы теории движения во времени, которая находится еще в зачаточном состоянии!
Похоже, что в природе существуют мощные источники энергии, освобождающейся при замедлении движения тел во времени. Это не только "черные дыры", в которых определенно идет этот процесс. Думается, что он идет и в недрах Солнца, может быть, даже и в недрах Земли в какой-то степени. Ведь давно известно, что в ней существуют какие-то неучтенные источники энергии.
До последнего времени источником энергии излучения Солнца считались реакции термоядерного синтеза, идущие в его недрах. Но они должны были сопровождаться выделением огромного количества нейтрино - всепроникающих безмассовых частиц, движущихся, как до сих пор считают почти все физики, со скоростью света С. (В книге [9] выдвинута гипотеза, что нейтрино летят со сверхсветовыми скоростями.) В 60-е годы сначала в США, а затем в СССР построили большие установки для регистрации солнечных нейтрино, но оказалось, что их поток по крайней мере в 3 раза ниже ожидавшегося. С тех пор ученые теряются в догадках.
Так, может быть, действительно основным источником энергии Солнца являются не термоядерные реакции, а просто разогретое вещество высвечивает часть энергии движения во времени?
Но для этого ей надо каким-то образом превратиться не в энергию движения в пространстве Ev, а в кинетическую энергию атомов Ек. Последняя, как мы уже видели, не идентична Ev, а является ее составной частью.
В СТО кинетической энергией E. называют энергию, определяемую формулой (3.3). Не будем ломать эту традицию, хотя член-корреспондент PAEH "нерелятивист" В. M. Мигунов [18], а вслед за ним академик АЭН РФ Г. E. Иванченко [19],тоже пришедший к выводу об уменьшении внутренней энергии элементарных частиц с увеличением скорости их движения в пространстве, утверждают, что кинетической энергией тела следует называть разность энергий Ед, определяемую выражением (3.7).
Они уверяют, что энергия Ек, сообщаемая телу от движителя при ускорении движения тела в пространстве и называемая в СТО кинетической энергией, на самом деле затрачивается на деформацию пространства-времени (или эфира), в котором движется тело. При этом Мигунов пишет, что энергия Eк идет на изменение гравитационной связи частицы со Вселенной и перераспределяется во Вселенной, со всеми телами которой частица находится в "динамическом равновесии" [18].
А у движущейся частицы, уверяет Иванченко, всегда остается только суммарная масса-энергия Е0 = Ет + Е∆, которая, по его мнению, инвариантна. Напомним, что в СТО тоже считают энергию покоя тела E0, инвариантом, не зависящим от скорости движения тела. Если бы это было действительно так, то на этом можно было бы закончить нашу книгу, так как это закрывало бы возможность превращения части массы покоя вещества в энергию излучения. Но, к счастью, это не совсем так, точнее, не всегда так, в чем мы убедимся в четвертой главе.

3.3. Экскурс в релятивистскую термодинамику

В книге [8] далеко не впервые было написано столь необычное для специалистов по теории относительности уравнение, получаемое из (3.4):

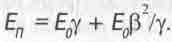(3.10)

Луи де Бройль еще в 1 967 году опубликовал в [20] очень похожее на него уравнение

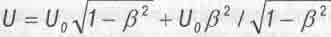(3.11)

которое получил простым алгебраическим преобразованием эйнштейновской формулы

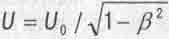(3.12)

Под U он здесь имел в виду энергию газа в баллоне, движущемся со скоростью ß, а под U0 - энергию того же газа в неподвижном баллоне. Де Бройль вывел уравнение (3.11), обсуждая известные формулы

(3.13)

полученные еще в 1907 г. М.Планком и М.Лауэ для релятивистского преобразован теплоты Q и температуры. Т при переходе от одной инерциальной системы отсчета к другой, движущейся относительно первой со скоростью ß.
Сам M. Планк выводил формулы (3.13) довольно сложным путем, приведенным например, в [21, 22] и основанном на предварительном доказательстве инвариантности давления газа и энтропии при преобразованиях Лоренца.
Необходимость возврата теоретиков в 60-е годы к широкому обсуждению форм (3.13), 50 лет не вызывавших сомнения у физиков, была обусловлена тем, что в 191 году появилась посмертная публикация Г. Отта [23], в которой обращалось внимание на то, что в некоторых случаях формулы (3.13) ведут к парадоксальным результата! и предлагалось заменить их формулами.

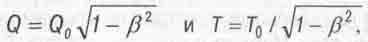(3.14)

Соответствующими Эйнштейновскому выражению (3.12) для полной энергии тела.
Дискуссия теоретиков продолжалась несколько лет, пока Луи де Бройль уравнением (3.11) не показал, что результаты Планка-Лауэ и Отта не противоречат друг - другу, а просто авторы разговаривают на разных языках. Ибо член 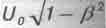в уравнении (3.11), совпадающий с формулой Планка-Лауэ (3.13), утверждал де Бройль, описывает переносимую телом при его движении тепловую энергию, а член 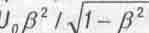описывает "Энергию переноса" этой тепловой энергии (или просто тепла) из одной инерциальной системы отсчета в другую.
К сказанному остается только добавить, что тепловая энергия газа в баллоне - это ведь часть внутренней энергии, содержащейся в баллоне, она является добавкой энергии покоя молекул, находящихся в баллоне. Поэтому формула (3.13) для тепло газа совпадает с нашей формулой (3.6) для внутренней энергии тела или энергии его движения во времени.
А то, что де Бройль назвал "энергией переноса", является не чем иным, как определяемой формулой (3.5) энергией движения в пространстве.
Таким образом, и де Бройль, и мы пришли разными путями к одному и тому же результату. Только великий французский физик на том и остановился в данном вопросе, рассматривая уравнение (3.11) лишь как вспомогательное.
И вообще участники той дискуссии 60-х годов считали, что рассматриваемые ими вопросы имеют исключительно теоретическое значение и далеки от насущных потребностей людей. Так, советский участник той дискуссии В.А. Угаров в [22] писал: "... формулы (3.13) имеют скорее принципиальное, чем практическое значение".
Такая убежденность основывалась на том, что при доступных людям технических скоростях движения макроскопических тел (например, баллонов с газом) релятивистский фактор ß = V/C чрезвычайно мал, а потому значения Q и Т, вычисляемые по формулам (3.13), оказывались практически неотличимыми от значений Q0 и Т0 даже при космических скоростях (V ~ 104 (10 в четвертой степени) м/с) движения тел.

Date: 2015-07-27; view: 826; Нарушение авторских прав