Выводы к главе

1. В матаматическом аппарате СТО, пренебрегший привилами теории комплексных чисел, допущен ряд ошибок. Самая важная из них - неправильное понимание интервала как расстояния - "путь", проходимый телом в собственном времени за время движения этого тела в пространстве, выраженный в единицах длины.
2. Скорость движения тела во времени 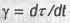следует определять подпбно скорости движения его в пространстве 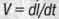как производную от пути по времени t, измеряемому наблюдателем, относительно которого движется данное тело.
3. точку пространства - времени следует описывать не комлексным числом 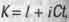, как это делал Г. Минковский, а комплексным числом 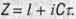. Это значит, что четвертой осью координат пространства - времени является ось , а не ось .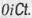
4. Безразмерная скорость движения тела во времени y и безразмерная скорость движения его в пространстве 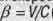(где С - скорость света в вакуума) связаны основным уравнением теории движения .
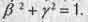5. Кроме действительных решений (попарных чискел 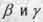), графиком которых является единичная окружность, основное уравнение теории движения имеет еще два семейства мнимых решений, гкафиками которых являются гиперболы. При мнимых y основное уравнение описывает движение частиц со сверсветовыми скоростями 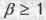(тахионов), а при мнимых ß - вращательное движение тела, имеющего в результате вращения скорость движения во времени y больше единицы.

Глава вторая

ЭЛЕМЕНТЫ ДИНАМИКИ ДВИЖЕНИЯ ВО ВРЕМЕНИ

2.1. Закон сохранения количества движения во времени

Все мы понимаем, что непрерывно движемся во времени из прошлого в будущее вместе с окружающими нас предметами. Тем не менее до сих пор не существует целостной теории движения во времени. Рождение таковой задерживало, как ни странно, изобретение часов. Ибо с появлением механических часов, стрелки которых "идут" мелкими шагами, люди стали говорить не о движении времени, а о "ходе времени", как еще раньше, с изобретением водяных и песочных часов - клепсидр, начали говорить о "течении времени", наблюдая за течением воды или песка в этих часах.
Поэтому, когда в 1905 г. А. Эйнштейн предложил СТО, он заявил, что из нее следует, что ход времени зависит от скорости движения в пространстве. Про движение во времени даже речи не было. Эйнштейн изучал закономерности движения в пространстве, а затем и само пространство. Исходя из только-только открытого тогда факта, что в природе не существует скоростей, больших скорости света в вакууме С, он говорил о "ходе времени".
Лишь в 1908 г. Г. Минковский, помогавший Эйнштейну разрабатывать математический аппарат теории относительности, догадался, что пространство и время взаимосвязаны, и объединил их в единое четырехмерное пространство-время, в котором движутся все тела.
Однако четырехскорость Минковского, о которой мы говорили в разделе 1.2, была далеко не лучшим изобретением СТО - ее недостатки слишком бросались в глаза. Поэтому после смерти Минковского в 1909 г. этим понятием пользовались редко. Потому-то все до сих пор говорят о "ходе времени", а не о движении во времени, упуская из-за этого из вида динамические параметры движения тел во времени.
Это все равно, что говорить "бег дороги" вместо "бег автомобиля по дороге". Некоторые скажут, что не видят особой разницы между этими двумя выражениями, поскольку движение - понятие относительное. Но все же на повороте заносит авто-обиль, а не дорогу. Поэтому для безопасного движения автомобиля учитывают его скорость и массу (произведение этих величин называют импульсом), а не массу дороги.
Мы уже говорили, что Е. Л. Фейнберг в [7] выражал беспокойство о том, что адиционный кинематический подход к СТО делает ее формальной наукой. Он указал, что для улучшения понимания предмета надо бы исходить из динамических хактеристик движения, и сетовал, что этого никто не сделал. Но сделать это, исхо-
13 динамических характеристик движения тел в пространстве, было, по-видимому, невозможно, а рассматривать динамические характеристики мнимого движения во времени никому, увы, и в голову не приходило до появления работы [8].
В ней впервые было показано, что если учесть динамические параметры движения тел во времени, как учитывают аналогичные параметры движения автомобиля по дороге, то в СТО, столь трудной для понимания, все становится очень простым и ясным.
Хотя мнимого движения тел во времени мы не видим, попробуем представить, чти оно в какой-то мере подчиняется законам обычной классической механики, в которой скорость V перемещения тела в пространстве заменим скоростью у движения его во времени. По аналогии с известным уравнением закона сохранения обычного импульса (количества движения) Р = mV в системе центра инерции

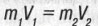(2.1)

составим уравнение для закона сохранения количества движения тела во времени:

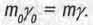(2.2)

Здесь m0 - масса неподвижного в пространстве тела (масса покоя), т - масса того же тела при движении его в пространстве.
Мы воспользовались частным случаем уравнения для закона сохранения импульса (2.1). В нем m1 и V, - это, например, масса и скорость пули, а m2 и V2 - соответственно масса винтовки и скорость отдачи, приобретаемой винтовкой при выстреле. Это же уравнение (2.1) описывает и закон сохранения импульса вагона, свободно катящегося по рельсам под мостом, с которого в вагон насыпают песок. Если до моста масса вагона была та скорость V1, то после моста масса вагона с песком возрастает до m2. При этом импульс вагона Р остается неизменным.
То же самое справедливо и при движении тела во времени. Только теперь не скорость движения является функцией от массы движущегося тела, как было в примере с вагоном, а наоборот: величина массы тела зависит от скорости у движения данного, тела во времени. Это и отражает уравнение (2.2) и получаемая из него простым алгебраическим преобразованием известная в СТО формула для релятивистской массы

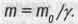(2.3)

Ее вывод в учебниках по СТО особенно сложен. Мы же получили ее почти шутя, учитывая, что у = 1.
Из (2.3) понятно, что масса тела возрастаете увеличением скорости У его движения в пространстве. (Так как 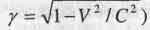. СТО объясняет, что это увеличение массы тела вызывается тем, что в массу превращается кинетическая энергия, сообщаемая телу при его ускорении. А вот из теории движения не только понятна причина возрастания массы, но и объясняется закон, по которому происходит это увеличение массы. Оно обусловлено действием закона сохранения количества движения тела во времени. Это один из важнейших законов природы наряду с хорошо всем известным законом сохранения обычного импульса.
Вооружившись законом сохранения-количества движения во времени, мы теперь можем приступить к реализации мечты Е. Л. Фейнберга о выводе основных уравнений формул СТО исходя из динамических характеристик движения тел. Посмотрим, например, что происходит с размерами тел при их движении в пространстве-времени. Для этого домножим обе части уравнения (2.2) на некоторую длину l 0, измеренную вдоль направления движения тела в пространстве. Этим мы превратим данное уравнение в уравнение для закона сохранения момента количества движения тела во времени:

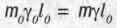(2.4)

Вектор мнимой скорости l движения тела во времени всегда перпендикулярен вектору действительной скорости ß движения его в пространстве, поскольку векторы действительной и мнимой частей вектора J, изображающего комплексное число на комплексной плоскости, всегда ортогональны. Значит и соответствующие им векторы действительного (m ß) и мнимого (mу) импульсов также взаимно перпендикулярны. А длину отрезка l0 мы выбрали вдоль вектора m ß значит, перпендикулярно мнимому вектору ту. Поэтому векторное произведение вектора mу на перпендикулярный ему радиус-вектор l0 есть не что иное, как момент мнимого количества движения во времени относительно начала отрезка l0. Само же уравнение (2.4) выражает закон сохранения момента количества движения тела во времени.
Обозначим произведение l0у в уравнении (2.4) как некую новую длину l, а величину m заменим ее значением m0lу из формулы (2.3). Тогда уравнение (2.4) превратится в тождество, и мы тем самым докажем известную формулу СТО для лоренцева сокращения длин при движении тел:

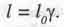(2/5)

Как видим, она тоже выводится из закона сохранения количества движения тела во времени. Это один из основных законов физики, вытекающий, как и закон сохранения обычного импульса, из общепризнанного постулата об однородности пространства Вселенной.
Если же мы возьмем отрезок l0 не вдоль, а перпендикулярно направлению щижения тела в пространстве, то векторное произведение l0 на mу будет равно нулю при любых значениях у (как векторное произведение параллельных векторов).
Поэтому в последнем случае l1 = l0 при любых у. То есть размеры тел в направлениях, перпендикулярных направлению их движения в пространстве, остаются неизменными при любых скоростях движения.
Ну а формулу СТО для релятивистского замедления хода времени на движущихся телах

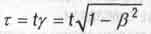(2.6)

нам и выводить не надо. Она непосредственно вытекает из данного в разделе 1.3 определения безразмерной скорости у.
Разберем теперь, что такое преобразования Лоренца, о которых уже упоминалось выше. Когда вы едете в поезде и находитесь на расстоянии X' от задней стенки последнего вагона, то расстояние от Вас до станции, от которой отъехал поезд, составляет:

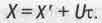(2.7)

Здесь U - скорость поезда, г- время в пути. Такие вычисления в классической механике называют преобразованиями Галилея при переходе от движущейся к неподвижной системе отсчета координат. Много веков считалось, что при переходе от движущейся к неподвижной системе отсчета остаются неизменными длины отрезков и время, а вот скорости движения суммируются геометрически как векторы. Так, скорость Вашего движения по вагону суммируется со скоростью поезда, и относительно столба на обочине дороги Вы движетесь уже с большей скоростью, чем относительно вагона.
В конце XIX века результаты опыта Майкельсона указали, что свет от фар едущего паровоза летит вперед относительно паровоза с такой же скоростью, с какой он летит, в тот же момент и относительно столба на обочине дороги. Это открытие потрясло физиков. Начались поиски таких преобразований координат, которые оставляли бы скорость света С неизменной при переходе от движущейся к неподвижной системе отсчета. Они были найдены в 1904 г. X. Лоренцем.
Поскольку мы уже знаем, как зависят длина тела и ход времени на нем от скорости движения тела в пространстве, то для нас уже не составит особого труда вывести: формулы преобразований Лоренца.
Для едущего в поезде наблюдателя кажется, что это не поезд едет, а окрестным поля и леса движутся относительно него в обратную сторону со скоростью - U. Поэтому расстояния Х до станции (отмеченные верстовыми столбами вдоль дороги) на движущейся относительно него земле подвергаются лоренцевому сокращению по формуле (2.5) и становятся для него равным Х'=Х у, где 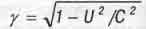- скорость движения поезда во времени. Тогда вышеприведенное выражение для преобразования Галилея (2.7) превращается в формулу преобразования Лоренца, для пространственных координа:

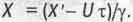(2.8)

А формулу преобразования Лоренца для времени выведем из вышеприведенного выражения (2.6), возведя его в квадрат и разделив обе его части на t. Учтя, что 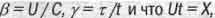получим:

(2.9)

Здесь - время, измеряемое собственными часами пассажира поезда, а t -время, измеряемое часами на станции. Понятно, что, когда поезд был еще на станции (Х= 0), показания обоих часов совпадали.
Ну и, наконец, выведем формулу сложения скоростей СТО, которая даст ответ на вопрос, почему столь странные результаты получились в опыте Майкельсона и в; опытах Физо. Когда пассажир поезда шагает вперед по ходу поезда со скоростью V' относительно вагона, то расстояние X' пройденное пассажиром в вагоне за собственное время т, измеренное часами в вагоне, составит величину X'= 1/ . Подставим это выражение вместо X' в формулы (2.8) и (2.9), а затем разделим (2.8) на (2 9) В результате получим формулу для суммарной скорости движения пассажира относительно земли, по которой едет поезд:

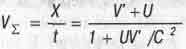(2.10)

(Эту формулу сложения скоростей за 7 лет до Эйнштейна опубликовал Дж. Лармор.) Из найденной формулы понятно, что, поскольку скорости V' и U не могут превышать величину скорости света С, то суммарная скорость VЕ ни при каких обстоятельствах не превысит скорость света в вакууме С.
Начав этот раздел с разговора о количестве движения во времени, давайте и закончим его разговором об этом мнимом импульсе mу. Домножив обе части уравнения (1.16) на m2с2(m квадрат с квадрат) и вспомнив, что mу = m0у0, получим выражение:

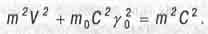(2.11)

Из него видим, что сложение реального импульса движения тела в пространстве Р = mV и мнимого импульса движения того же тела во времени mС у = m0С у 0 осуществляется по правилу сложения взаимно перпендикулярных векторов. Это еще раз напоминает нам, что указанные импульсы, как и соответствующие им скорости движения тела в пространстве и во времени, всегда взаимно ортогональны как реальная и мнимая части комплексного числа.
А домножив почленно обе части уравнения (2.11) на С2(c квадрат), получим известное в СТО уравнение:

(2.12)

связывающее полную энергию тела Еn = mС2(c квадрат) с его массой покоя ту и импульсом Р. Только здесь эти формулы несут гораздо больше информации, чем в СТО.
Эти формулы скоро понадобятся нам. А отсылать читателя за ними к учебникам по СТО мы постеснялись, ибо тогда ему пришлось бы "перелопатить" десятки страниц, и неизвестно еще, с каким результатом. Наш же вывод с помощью теории движения во времени занял всего несколько страниц. Надеемся, что преподаватели физики с Удовольствием возьмут его на вооружение. Это позволит им и их слушателям экономить немало времени даже без "машины времени", к изобретению которой (чем черт не шутит!) может привести дальнейшая разработка теории движения во времени.

Date: 2015-07-27; view: 785; Нарушение авторских прав