Теорема Абеля

Пусть ряд 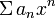сходится в точке . Тогда этот ряд сходится абсолютно в круге 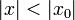и равномерно по 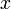на любом компактном подмножестве этого круга.

Обращая эту теорему, получаем, что если степенной ряд расходится при 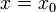, он расходится при всех 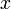, таких что 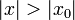. Из первой теоремы Абеля также следует, что существует такой радиус круга 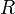(возможно, нулевой или бесконечный), что при 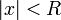ряд сходится абсолютно (и равномерно по 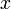на компактных подмножествах круга 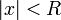), а при 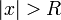— расходится. Это значение 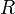называется радиусом сходимости ряда, а круг 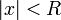— кругом сходимости.

Для степенного ряда 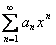радиус R (половина длины) интервала сходимости можно вычислить по формуле Коши-Адамара:

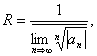
причем считают, что если этот верхний предел равен нулю, то ряд сходится на всей числовой оси (радиус сходимости бесконечен), а если предел равен бесконечности, то радиус сходимости равен нулю. На каждом из концов этого интервала ряд может как сходиться (абсолютно или условно), так и расходиться. Вне этого интервала ряд расходится. Заметим, что интервал сходимости существует для каждого сходящегося хоть на каком-нибудь интервале степенного ряда. Для ряда, сходящегося только в одной точке, интервал получается вырожденным. Для расходящегося ряда интервал равен пустому множеству.

Ряды Тейлора и Маклорена

Если функция f (x) имеет непрерывные производные вплоть до (n+ 1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора: 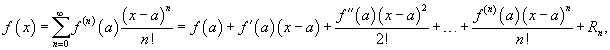где Rn − остаточный член в форме Лагранжа определяется выражением 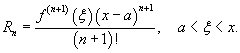Если приведенное разложение сходится в некотором интервале x, т.е. 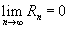, то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a. 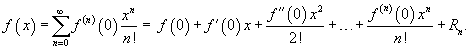Если a = 0, то такое разложение называется рядом Маклорена: Разложение некоторых функций в ряд Маклорена · · · · ·

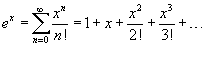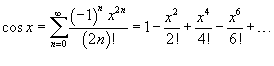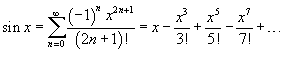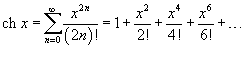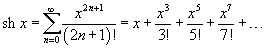
Date: 2015-07-27; view: 451; Нарушение авторских прав