Дискретные системы

В линейной непрерывной системе входной и выходной сигналы связаны дифференциальным уравнением. В дискретной линейной системе связь между дискретным входом 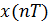и дискретным выходом определяется разностным уравнением вида:

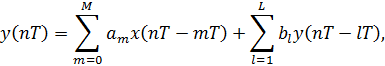
где (M+1) – число прямых связей,

L – число обратных связей.

Структурная схема, соответствующая уравнению (6.1) имеет вид:

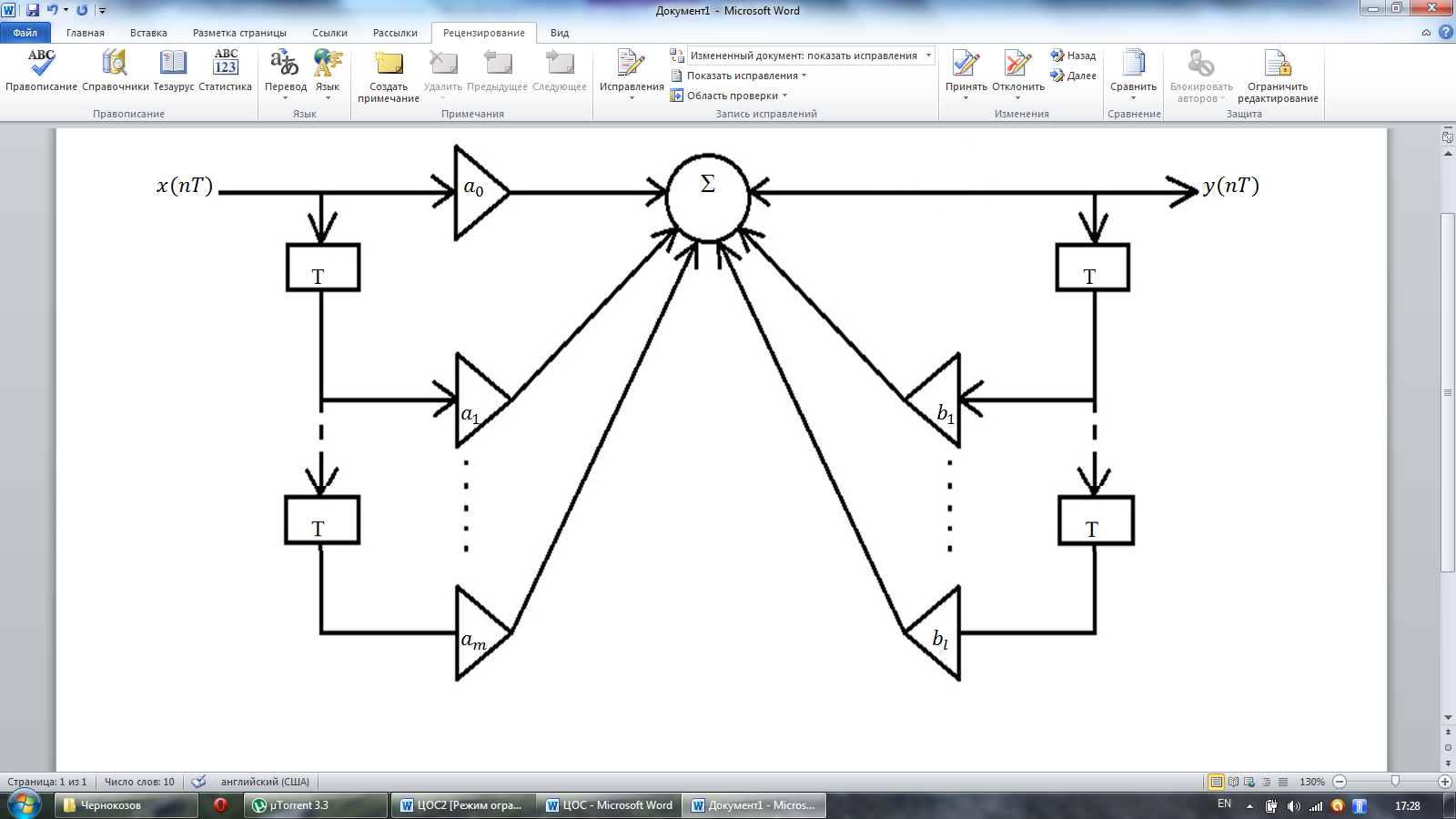
Рисунок 6.1

Пример 6.1 - Определить 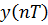, если 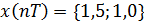и дискретная система имеет вид:

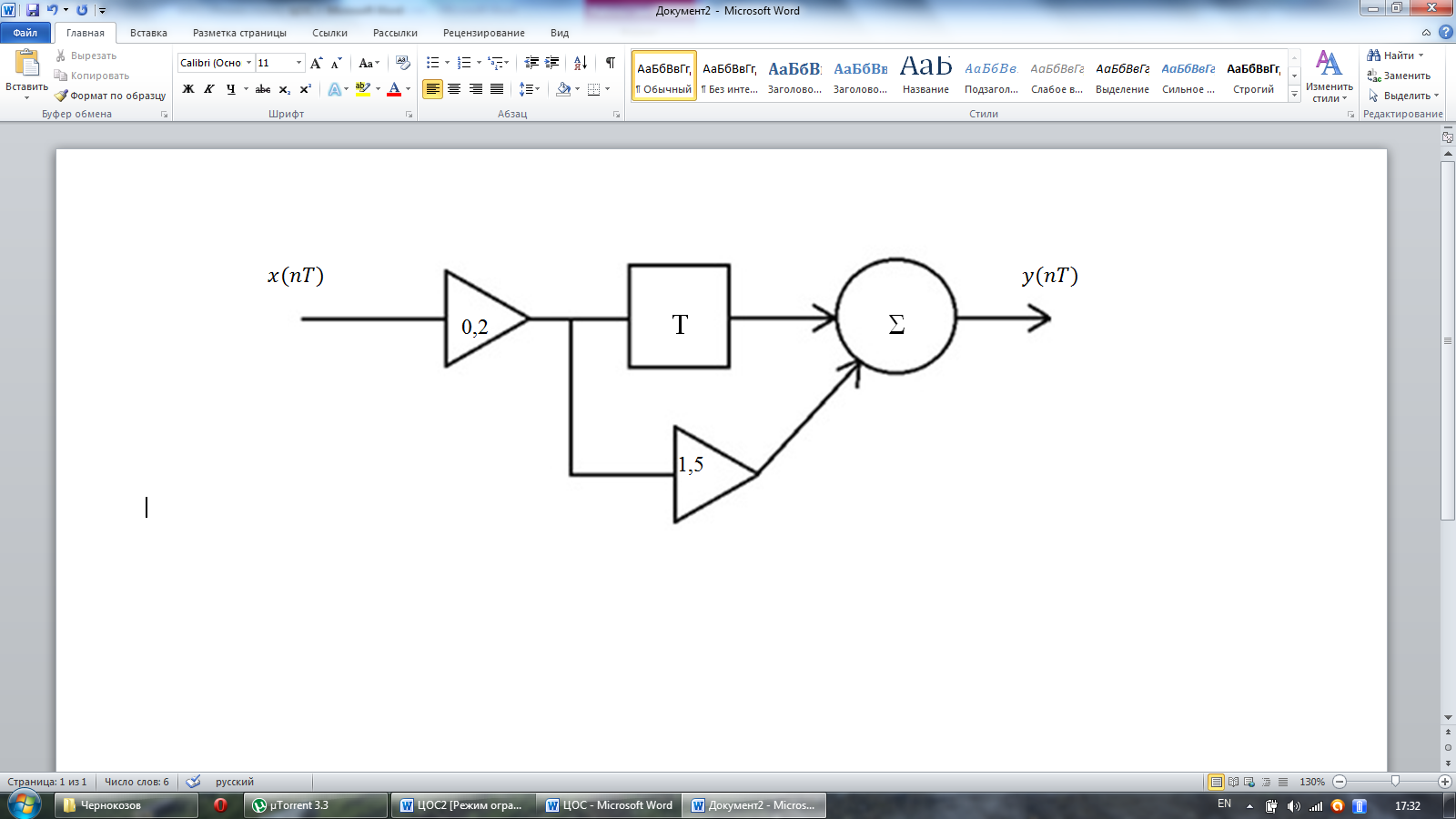
Решение. Система без обратной связи описывается разностным уравнением:

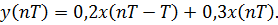
Решая уравнение для заданного входного сигнала, получим:

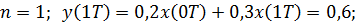
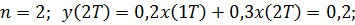
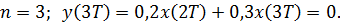
Графики входного и выходного сигналов:

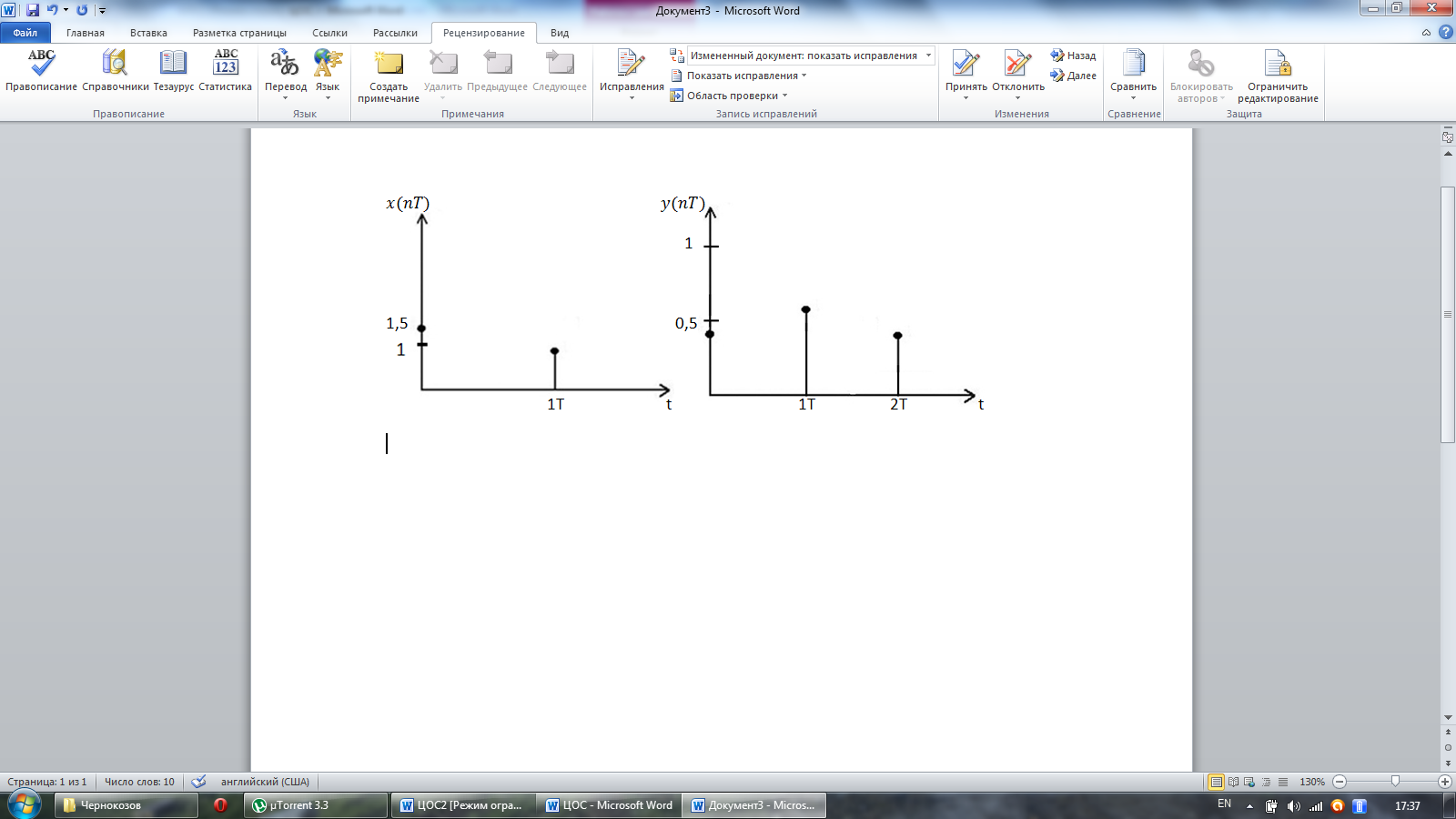
а) б)

Рисунок 6.2

Пример 6.2 - Определить 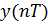, если 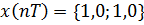и дискретная система имеет вид:

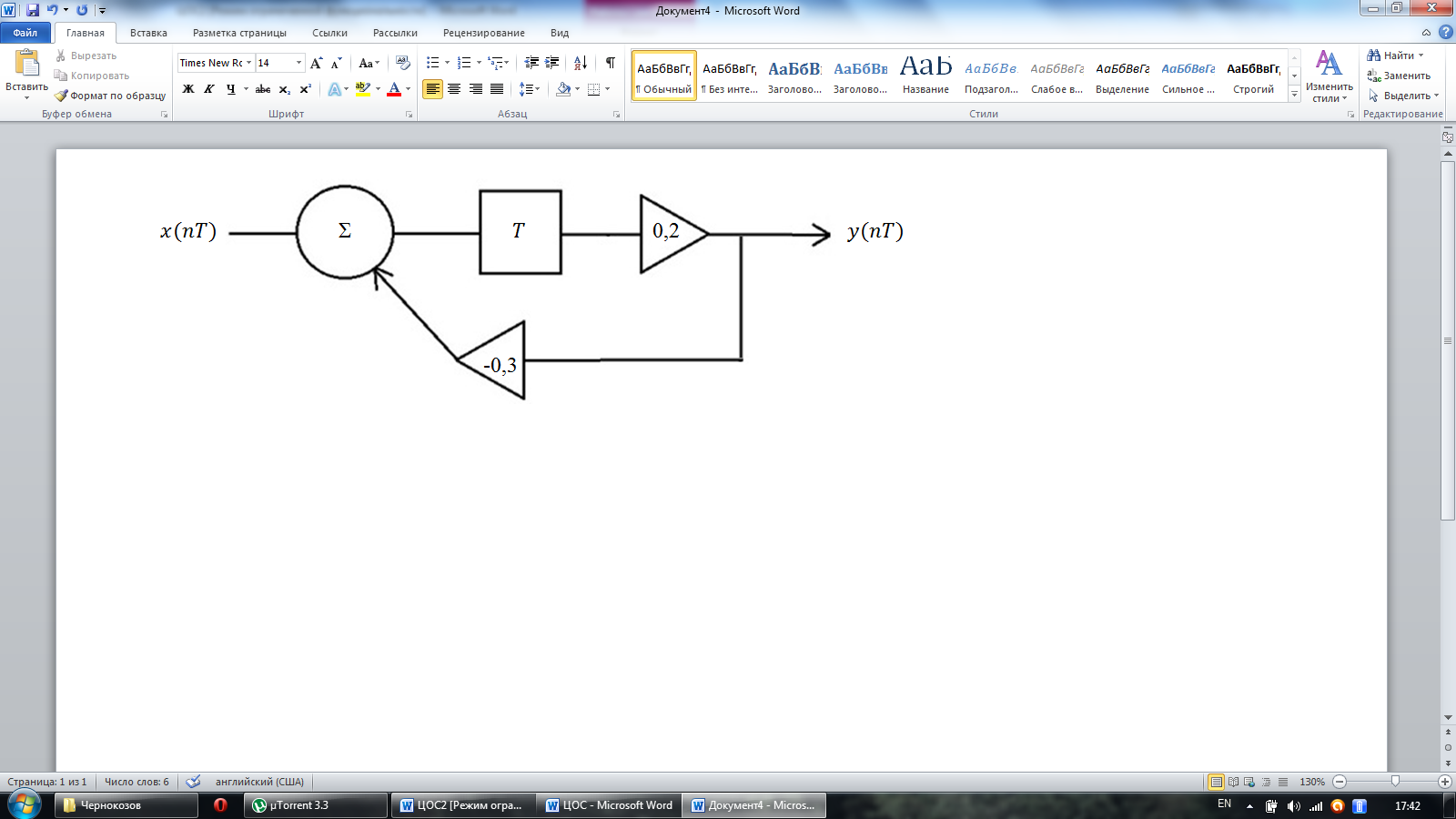
Рисунок 6.3

Решение. Разностное уравнение системы с обратной связью имеет вид:

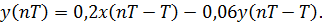
Выходной сигнал будет иметь вид:

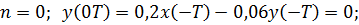
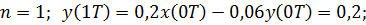
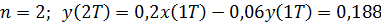
и т.д.

Переход к z-изображениям сигналов в (6.1) приводит к алгебраизации разностного уравнения. Учитывая теоремы линейности и запаздывания, получим:

Передаточная функция 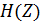дискретной системы определяется как отношение Z-изображения выходного сигнала к Z-изображению входного:

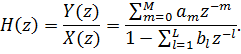
При отсутствии обратных связей, в частности, получим:

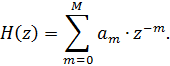
Пример 6.3 - Определить передаточную функцию дискретной системы (рис. 6.4).

Решение.

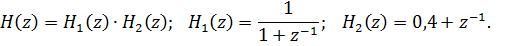
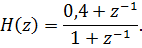
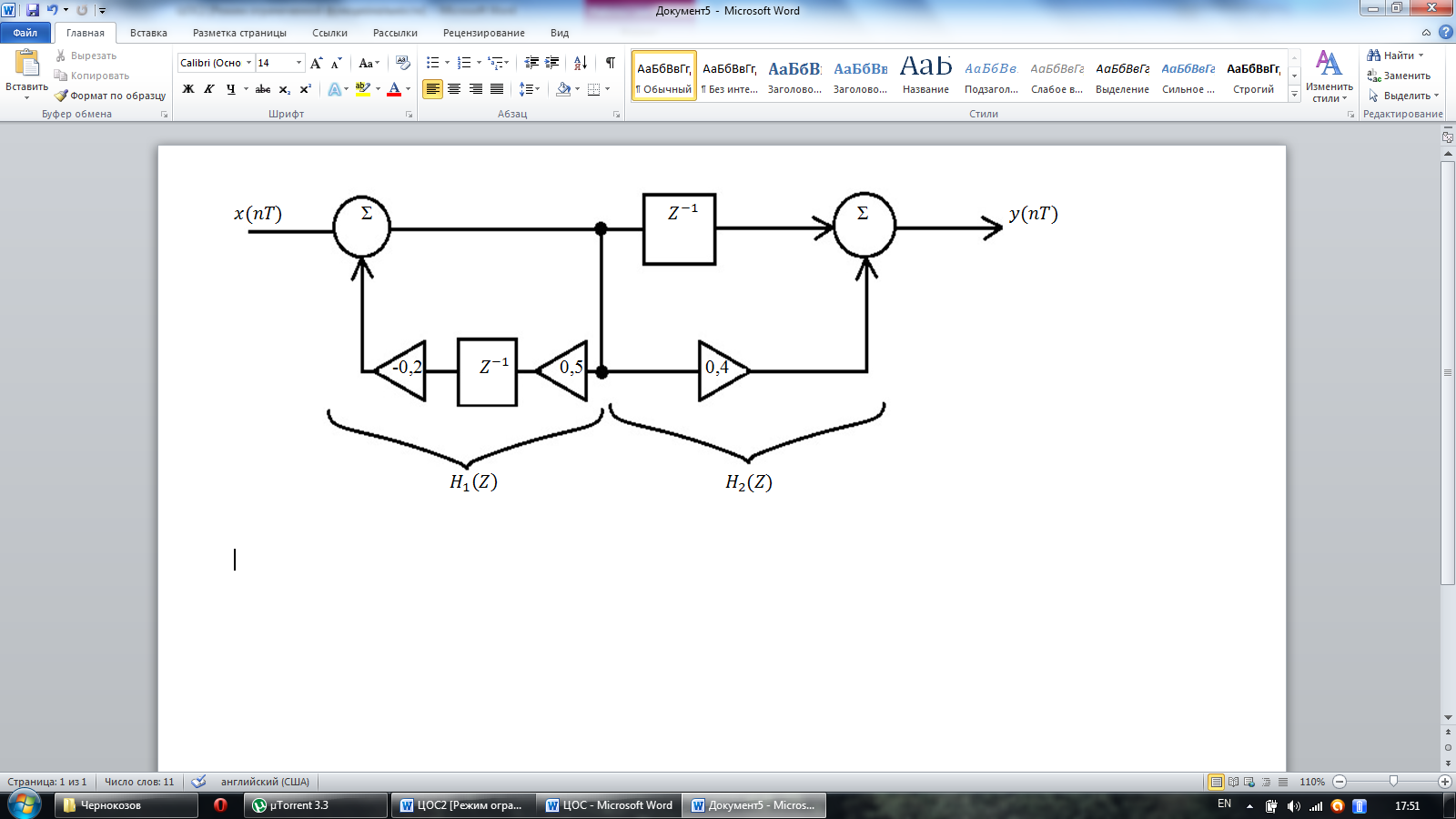
Рисунок 6.4

Комплексный коэффициент передачи и частотные характеристики дискретной системы определяются из передаточной функции:

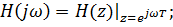
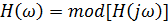– амплитудно-частотная характеристика (АЧХ);

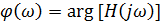– фазо-частотная характеристика (ФЧХ).

Пример 6.4 - Определить частотные характеристики дискретной системы, передаточная функция которой: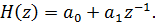

Комплексный коэффициент передачи:

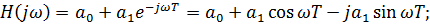
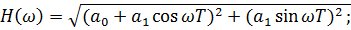
Графики АЧХ и ФЧХ для :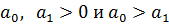

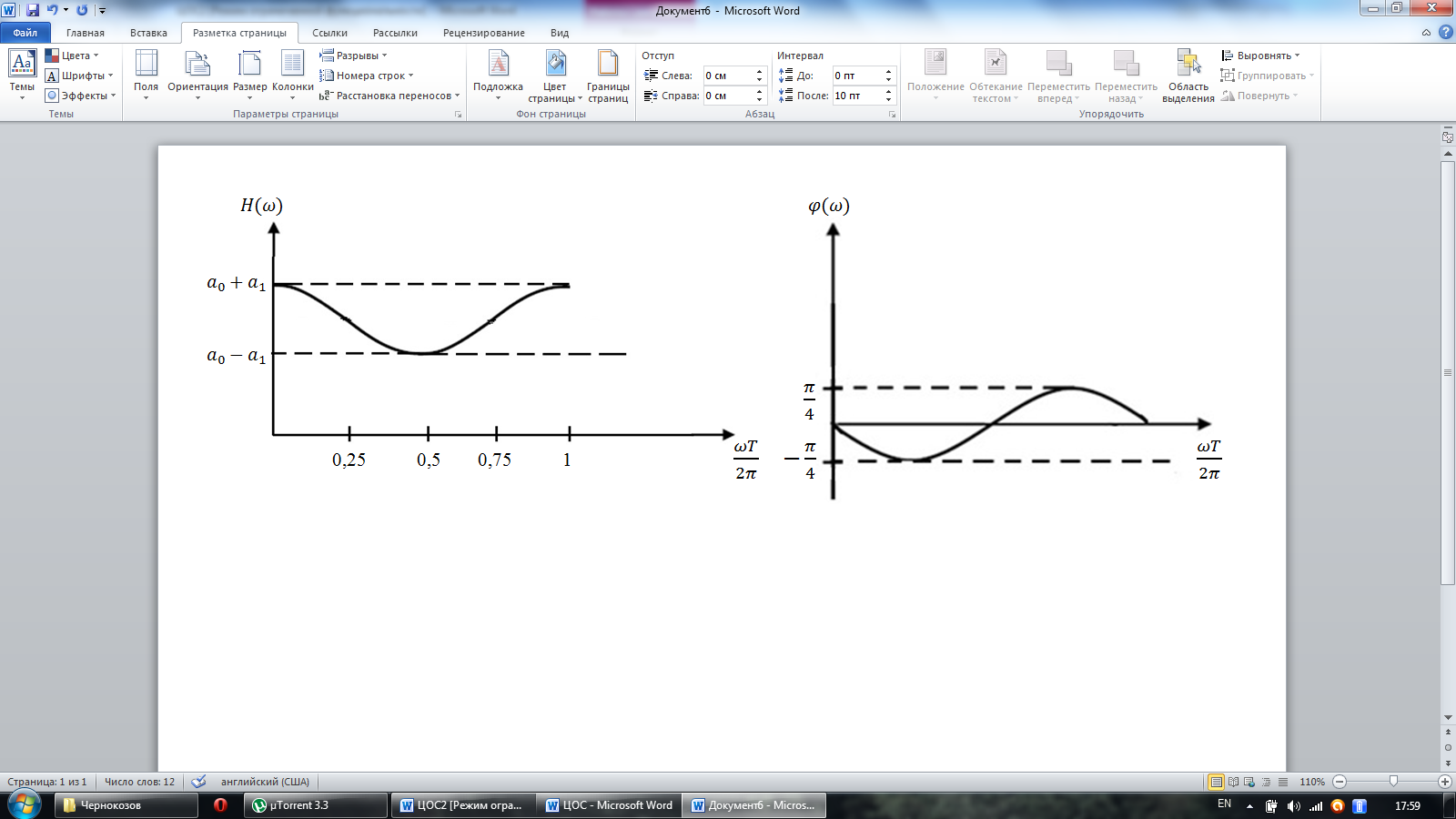
Рисунок 6.5

Во временной области дискретная система характеризуется импульсной характеристикой, т.е. реакцией на дискретную 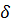- функцию.

Импульсную характеристику системы можно определить решением разностного уравнения, полагая 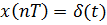, или по передаточной функции, разделив полином числителя на полином знаменателя.

Пример 6.5 - Определить импульсную характеристику системы, представленной на рис. 6.3.

Решение. Разностное уравнение системы:

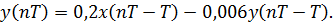
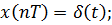
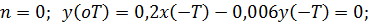
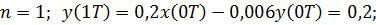
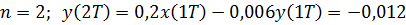и т.д.

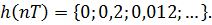
Пример 6.6 - Определить импульсную характеристику системы, представленной на рис.6.3 по передаточной функции.

Решение.

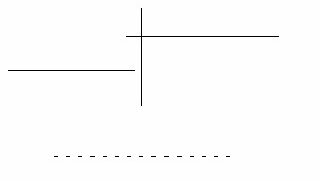
0,2 z+0,06

0,2+0,01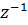2 0,2 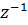-0,012

-0,012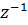

-0,012 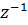-0,00072

Применяя теорему запаздывания, получим:

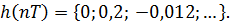
Сравнивая результаты с предыдущим примером, убеждаемся в достоверности расчетных методов.

Из определения передаточной функции следует, что в частотной области сигнал на выходе, равен:

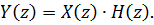
По теореме о свёртке, выходной сигнал во временной области:

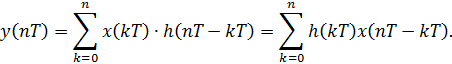
Это выражение определяет алгоритм работы дискретных систем.

Пример 6.7 - Определить сигнал на выходе дискретной системы, изображенной на рис.6.3, если

Решение. 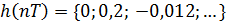(см. предыдущий пример).

Из (6.6) получим:

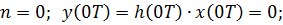
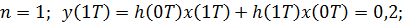
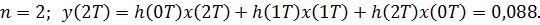
Таким образом .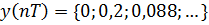

При реализации цифровых систем вместо линейной свёртки (6.6) чаще применяется круговая или циклическая свёртка.

Цифровая обработка в частотной области требует периодичности сигнала и импульсной характеристики системы во временной. Только в этом случае получаются числовые последовательности, описывающие спектральные характеристики, как сигнала, так и системы. Однако реальные сигналы и импульсные характеристики реальных систем, как правило, не периодические и более того – не конечные. Искусственно ограничивая числовые последовательности во временной области и продолжая их путем периодического повторения, можно выполнить условие цифровой обработки спектральных характеристик. При этом числовые последовательности, как сигнала, так и системы будут связанны формулами дискретного преобразования Фурье. Свёртка во временной области в пределах одного периода N называется круговой и имеет вид:

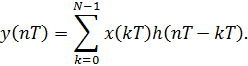
Период 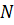выходного сигнала равен:

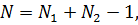
где 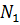– длина последовательности ,

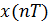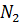– длина последовательности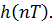

Так как исходные числовые последовательности сигнала и системы должны иметь периоды равные 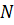, то их необходимо доопределить нулями.

Пример 6.8 - Вычислить круговую свёртку по данным примера 6.7.

Решение. Представить импульсную характеристику системы конечной числовой последовательностью вместо 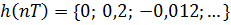в примере 6.7.

Так как 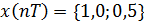, то с учетом (6.8):

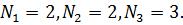
Исходные числовые последовательности будут иметь вид:

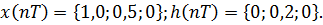
Из (6.7) получаем:

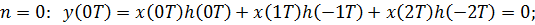
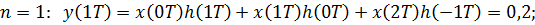
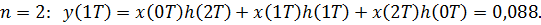
Таким образом 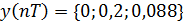, что совпадает с расчетами в примере 6.7 для линейной свёртки.

Для периодических числовых последовательностей остается в силе замена свёртки во временной области умножением спектров сигнала и импульсной характеристики в частотной области, используя дискретное преобразование Фурье.

Date: 2015-07-27; view: 671; Нарушение авторских прав