II. Теоретическая часть

1. Необходимость дальнейшего расширения множества чисел связана в основном с двумя причинами. Во-первых, рациональных чисел недостаточно для выражения результатов измерений (например, нельзя выразить рациональным числом длину диагонали квадрата со стороной 1). Во-вторых, такие числовые выражения, как 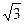, , 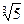sin 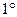и т.д., не являются рациональными числами. Объединение множества рациональных чисел и множества иррациональных чисел (бесконечных десятичных непериодических дробей) дает множество R действительных чисел. 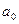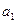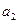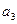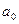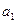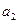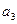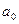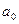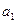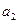Действительным числом называется бесконечная десятичная дробь, то есть дробь вида + , … или - , …, где -целое неотрицательное число, а каждая из букв , 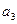…- это одна из десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

2. Арифметические операции над действительными числами обычно заменяются операциями над их приближениями.

Например, 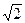=1,4142135…

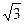=1,7320508…

Вычислим сумму

с точностью до единицы:

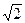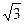
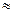+ 1,4+1,7=3,1 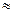3;

с точностью до десятой:

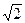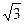
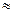+ 1,41+1,73=3,14 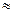3,1;

с точностью до сотой:

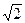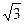
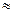+ 1,414+1,732=3,146 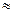3,15 и т.д.

Числа 3; 3,1; 3,15 и т.д. являются последовательными приближениями значения суммы + .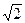

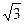Пусть 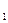х 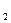, х …,х …- последовательные приближения действительного числа х с точностью до 1, до 0,1, до 0,01 и т.д. Тогда погрешность приближения 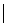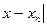как угодно близко приближается к нулю.

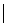
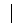
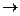0 при n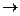

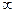
Или 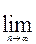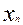=х

3. Все основные действия над рациональными числами сохраняются и для действительных чисел (переместительный, сочетательный и распределительный законы, правила сравнения, правила раскрытия скобок и т.д.).

4. Модуль действительного числа x обозначается 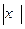и определяется так же, как и модуль рационального числа:

=

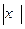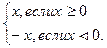
III. Практическая часть.

№6 – устно.

Ответ: 3),4).

№8(1) – учитель объясняет решение.

Найдем целые приближения 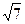с недостатком и избытком:

2< 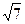<3.

Тогда 5- 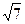>0, следовательно, 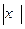=х.

(2) – под диктовку.

(3) – устно.

Ответ: 2) 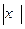=-х, 3) 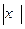=х.

№9(1, 3, 5) – по очереди на доске.

Ответ: 1)рациональное, 3)рациональное, 5)рациональное.

№10(1) – учитель с классом. (Учитель записывает на доске решение, которое «создается» учащимися:

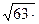
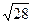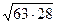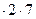= = =3 =42.)

№10(2) – устно.

№10(3) – на доске по желанию.

№10(4) – за доской.

Ответ: 1)42; 2)10; 3)2,5; 4) .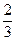

№11(1) – самостоятельно. (Указание: найти последовательные приближения сумм:

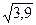=1,974… 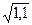=1,048…

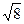=2,828… =4,123…

Ответ: + > + .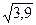

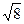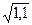№12 – работа в группах. Класс делится на группы по 3-4 человека в каждой. Количество групп кратно трем. Группы №1, 4 и т.д. выполняют первое задание, группы №2, 5 и т.д. – второе, группы №3, 6 и т.д. – третье. Учитель записывает на доске номера групп. По мере выполнения задания представитель группы выходит к доске и записывает получившийся ответ возле номера своей группы.

Ответ:1) 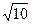; 2)3; 3)2+ .

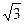IV. Домашнее задание: №9(2, 4, 6), №11(2), №93.

V. Итог урока. Провести самоанализ (Чему я научился на этом уроке: что нового узнал?)

Date: 2015-07-25; view: 968; Нарушение авторских прав