
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Порядок выполнения работы. Прежде всего проверим, имеет ли игра седловую точку
|
|
Прежде всего проверим, имеет ли игра седловую точку. Для каждой стратегии игрока A найдем наименьший выигрыш 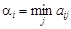
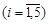 и запишем в соответствующий столбец:
и запишем в соответствующий столбец:
| B1 | B2 | B3 | B4 | a i | |
| A1 | |||||
| A2 | |||||
| A3 | –1 | –1 | |||
| A4 | |||||
| A5 | –2 | –2 | |||
| b j |
Рис. 1.3. Платежная матрица примера
Аналогично для каждой стратегии игрока B максимальный проигрыш 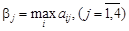 . Нижняя цена игры (максимин):
. Нижняя цена игры (максимин):
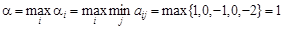 .
.
Верхняя цена игры (минимакс):
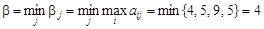 .
.
Максиминная (перестраховочная) стратегия игрока A есть стратегия A1. Применяя эту стратегию игрок A получит выигрыш не менее 1. Минимаксная (перестраховочная) стратегия игрока B есть стратегия B1. Применяя эту стратегию, он проиграет не больше 4.
Так как a ¹ b, будем решать игру в смешанных стратегиях. Цена игры при этом удовлетворяет условию 1 £ g £ 4.
Решение игры в смешанных стратегиях начинают с упрощения платежной матрицы и перевода всех ее элементов в область целых неотрицательных значений.
Поскольку соответствующие элементы второй и четвертой строк равны, то имеет место случай с дублирующими стратегиями. Следовательно, одну из строк можно убрать (например, четвертую). Элементы третьей строки меньше соответствующих элементов второй строки. Поэтому игроку А, стремящемуся максимизировать выигрыш, выгоднее применять стратегию А2, а не стратегию А3. В связи с этим опустим третью строку. Преобразованная матрица будет иметь следующий вид:
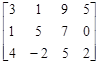 .
.
Элементы третьего столбца больше соответствующих элементов первого столбца. Поэтому стратегия B3 является для игрока B заведомо невыгодной. Опустим третий столбец и получим следующую матрицу:
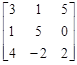 .
.
Анализируя эту матрицу, делаем вывод, что дальнейшему упрощению она не подлежит.
Для решения игры путем сведения к задаче линейного программирования, переведем элементы матрицы в область целых неотрицательных значений. Для этого прибавим к каждому элементу матрицы число 2 и получим следующую матрицу:
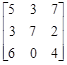 .
.
Составим задачу линейного программирования для игрока А:
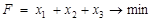 ,
,
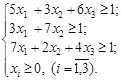 (1.10)
(1.10)
Для игрока B имеем двойственную задачу:
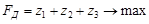 ,
,
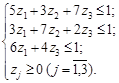 (1.11)
(1.11)
Для решения задачи (1.10) воспользуемся надстройкой Excel Поиск решения. Подготовьте исходные данные на листе Excel как показано на рис. 1.4.
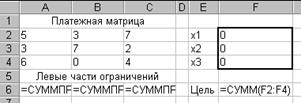
Рис. 1.4. Исходные данные для решения матричной игры
Ячейки F2:F4 отведены под значения переменных xi. В них введены начальные приближения, равные нулю. В ячейке F6 находится формула целевой функции (сумма переменных). В ячейках A6:C6 – формулы левых частей ограничений:
· A6: =СУММПРОИЗВ(A2:A4;$F$2:$F$4);
· B6: =СУММПРОИЗВ(B2:B4;$F$2:$F$4);
· C6: =СУММПРОИЗВ(C2:C4;$F$2:$F$4).
Формулу ячейки A6 в ячейки B6:C6 можно скопировать методом автозаполнения.
Вызовем надстройку Поиск решения и заполним диалоговое окно как показано на рис. 1.5 (необходимо также установить флажок Линейная модель, нажав кнопку Параметры).
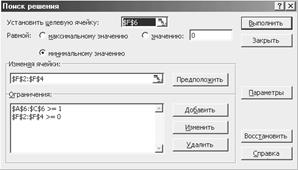
Рис. 1.5. Окно Поиск решения для решения матричной игры
Нажмем кнопку Выполнить, получим сообщение об успешном решении задачи и выберем в списке Тип отчета пункт Устойчивость. Переключатель должен быть установлен в положение Сохранить найденное решение. После нажатия кнопки OK Excel сформирует отдельный лист рабочей книги, содержащий отчет по устойчивости. Отчет по устойчивости требуется для того, чтобы не решать заново двойственную задачу: оптимальные значения двойственных переменных zj * приведены в графе Теневая цена этого отчета. Скопируем ячейки, содержащие значение теневой цены, на лист с исходными данными задачи в ячейки B8:B10 (рис. 1.6).

Рис. 1.6. Результаты решения игры
Найдем вероятности применения игроком А чистых стратегий по формуле
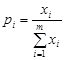 .
.
Для этого в ячейке H2 запишем формулу для нахождения p 1:
= F2/$F$6.
Вероятности p 2 и p 3 находятся аналогично, поэтому скопируем формулу из ячейки H2 в ячейки H3 и H4 с помощью автозаполнения.
Итак, 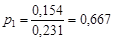 ,
,  ,
, 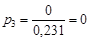 .
.
Вероятности применения игроком В чистых стратегий В j находим по формуле
 .
.
Для этого в ячейку D8 запишем формулу для нахождения q 1:
= B8/$F$6.
Вероятности q 2 и q 3 находятся аналогично, поэтому скопируем формулу из ячейки D8 в ячейки D9 и D10 с помощью маркера автозаполнения.
Итак, 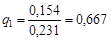 ;
; 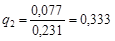 ;
; 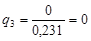 .
.
Цену игры найдем по формуле
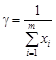 .
.
Однако это будет цена игры для преобразованной матрицы. Чтобы вернуться к исходной задаче, нужно вычесть 2 из g (так как ранее мы прибавляли двойку ко всем элементам платежной матрицы, а это увеличивает цену игры на 2). Итак, в ячейку F8 запишем формулу
=1/F6–2.
Получим, что цена игры равна 2,33. Учитывая, что для данной задачи a = 1, а b = 4, убеждаемся, что условие a £ g £ b выполнено.
Окончательно возвращаясь к исходной задаче, необходимо вспомнить, какие стратегии игроков A и B мы посчитали заведомо невыгодными и вычеркнули из платежной матрицы. Этим стратегиям, очевидно, соответствуют вероятности, равные нулю. Итак, для исходной платежной матрицы имеем следующие смешанные стратегии:
· игрока A: 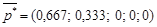 ;
;
· игрока B: 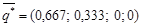 .
.
Полученные результаты можно сформулировать так: в случае многократного повторения игры игроку А для получения максимально возможного среднего выигрыша, равного 2,33, следует в приблизительно 67 % случаев применять первую стратегию, и в 33 % случаев – вторую. Например, если игра повторяется 100 раз, то 67 раз он должен применить первую стратегию и 33 раза – вторую. Остальные стратегии игроку А применять невыгодно.
Что касается игрока B, то он должен также применять свои первую и вторую стратегии в 67 % случаев и 33 % случаев соответственно. При этом его средний проигрыш будет 2,33, что значительно меньше верхней цены игры b = 4.
Date: 2015-07-25; view: 546; Нарушение авторских прав