Упрощение матричных игр

Если платежная матрица игры не содержит седловой точки, то задача определения оптимальной смешанной стратегии тем сложнее, чем больше размерность матрицы. Поэтому для игр с платежными матрицами большой размерности отыскание решения можно несколько упростить, если уменьшить их размерность путем вычеркивания дублирующих и заведомо невыгодных стратегий.

Определение 1. Если в матрице игры все элементы строки (столбца) равны соответствующим элементам другой строки (столбца), то соответствующие строкам (столбцам) стратегии называются дублирующими.

Определение 2. Если в матрице игры все элементы некоторой строки, определяющей стратегию А _i игрока А, не больше (меньше или равны) соответствующих элементов другой строки, то стратегия A _i называется заведомо невыгодной.

Определение 3. Если в матрице игры все элементы некоторого столбца, определяющего стратегию В _j игрока В, не меньше (больше или равны) соответствующих элементов другого столбца, то стратегия B _j называется заведомо невыгодной.

Для того, чтобы перевести значения всех элементов платежной матрицы в область неотрицательных значений, нужно ко всем элементам матрицы добавить некоторое достаточно большое число L. При этом цена игры g увеличится на L, а решение задачи не изменится.

Таким образом, платежную матрицу можно всегда преобразовать так, что ее элементы будут целыми неотрицательными числами, а это упрощает расчеты.

Пример. Выполнить возможные упрощения платежной матрицы:

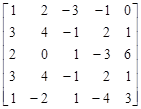. (1.1)

Решение. Поскольку соответствующие элементы второй и четвертой строк матрицы (1.1) равны, то имеет место случай с дублирующими стратегиями. Следовательно, одну из строк можно убрать (например, четвертую). Элементы первой строки меньше соответствующих элементов второй строки, а элементы пятой строки меньше или равны соответствующим элементам третьей строки. Поэтому игроку А, стремящемуся максимизировать выигрыш, выгоднее применять стратегии А₂ и А₃, а не стратегии А₁ и А₅. В связи с этим опустим первую и пятую строки, получим платежную матрицу (1.2):

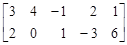. (1.2)

В преобразованной матрице (1.2) элементы первого и второго столбцов больше соответствующих элементов четвертого столбца. Поэтому игроку B, стремящемуся минимизировать проигрыш, стратегии В₁ и В₂ являются заведомо невыгодными. В связи с этим опустим первый и второй столбцы. По аналогичной причине после сравнения пятого и третьего столбцов опускаем пятый столбец. В результате приходим к матрице (1.3):

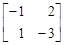. (1.3)

Далее, для того, чтобы перевести элементы матрицы (1.3) в область неотрицательных значений добавим к каждому из них число 4. Получим матрицу (1.4):

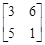. (1.4)

Сравнивая вновь строки полученной матрицы, заключаем, что дальнейшему упрощению она не подлежит.