
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Понятие игры, виды игр
|
|
В экономической и других сферах деятельности часто встречается проблема принятия управленческих решений в условиях неопределенности. При этом неопределенность может быть связана как с сознательными действиями противника, так и с другими факторами, влияющими на эффективность решения. Ситуации, в которых сталкиваются интересы двух и более конкурирующих сторон, преследующих разные цели, называются конфликтными. Математической теорией конфликтных ситуаций является теория игр.
Игрой называют математическую модель реальной конфликтной ситуации.В игре могут сталкиваться интересы двух (игра парная) или нескольких (игра множественная) противников; существуют игры с бесконечным множеством игроков. В данном пособии мы будем рассматривать только парные игры.
Игра ведется по определенным правилам. Каждый участник игры имеет несколько вариантов возможных действий (чистых стратегий). Из них он выбирает такие варианты, которые, как он полагает, могут обеспечить ему наилучший результат (исход игры). При этом каждый игрок имеет лишь общее представление о множестве допустимых ответных действий партнера, но не о его конкретном решении. В связи с этим ни один из игроков не может контролировать положение, поэтому как одному, так и другому игроку решение приходится принимать в условиях неопределенности. Непременным остается только стремление игроков использовать любую ошибку партнера в своих интересах. Игры, в которых оба участника, действуя в строгом соответствии с правилами, в равной мере сознательно стремятся добиться наилучшего для себя результата, называются стратегическими.
В экономической практике нередко приходится формализовать (моделировать) ситуации, в которых один из участников безразличен к результату игры. Такие игры называют статистическими или играми с природой. Под термином “ природа ” понимают всю совокупность внешних обстоятельств, в которых сознательному игроку приходится принимать решение.
Исход игры – это значение некоторой функции, называемой функцией выигрыша (платежной функцией). Платежная функция определяет для каждой совокупности выбранных игроками стратегий выигрыш каждой из сторон. Такая функция задается либо таблицей (платежная матрица), либо аналитическим выражением.
Если сумма выигрышей игроков равна нулю, то игру называют игрой с нулевой суммой. В случае парной игры это означает, что выигрыш одного игрока равен проигрышу другого.
1.1.2. Решение матричных игр в чистых стратегиях
(принцип минимакса)
Парную игру с нулевой суммой удобно исследовать, если функция выигрыша задается платежной матрицей.
Пусть игроки А и В располагают конечным числом возможных действий – чистых стратегий. Обозначим их соответственно А1, А2, …, А m и В1, В2, …, В n. Игрок А может выбрать любую чистую стратегию А i 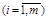 , а игрок В может выбрать любую чистую стратегию В j
, а игрок В может выбрать любую чистую стратегию В j 
 . Пара стратегий (А i, В j) однозначно определяет результат игры aij (aij – выигрыш игрока А или проигрыш игрока В при условии, если игрок A придерживается своей чистой стратегии A i, а игрок B – чистой стратегии B j). Если известны значения исхода игры aij для каждой пары (А i, В j) чистых стратегий, то можно составить платежную матрицу выигрышей игрока А (проигрышей игрока В) (рис. 1.1).
. Пара стратегий (А i, В j) однозначно определяет результат игры aij (aij – выигрыш игрока А или проигрыш игрока В при условии, если игрок A придерживается своей чистой стратегии A i, а игрок B – чистой стратегии B j). Если известны значения исхода игры aij для каждой пары (А i, В j) чистых стратегий, то можно составить платежную матрицу выигрышей игрока А (проигрышей игрока В) (рис. 1.1).
| B1 | … | B n | a i | |
| A1 | a 11 | … | a 1 n | a1 |
| … | … | … | … | … |
| A m | am 1 | … | amn | a m |
| b j | b1 | b n |
Рис. 1.1. Платежная матрица игры
Решить матричную игру означает определить наилучшую стратегию игрока A, а также наилучшую стратегию игрока B. Если рассматривается стратегическая игра, то предполагается, что противники одинаково разумны, и каждый из них делает все для того, чтобы добиться своей цели.
Используя этот принцип, найдем наилучшую стратегию игрока A. Выбирая стратегию A i, мы должны рассчитывать, что игрок B ответит на нее той из своих стратегий B j, для которой выигрыш игрока A будет минимальным. Найдем минимальное число aij в каждой строке матрицы:
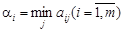 .
.
Эта величина есть гарантированный (самый малый) выигрыш игрока A при выборе им чистой стратегии A i. Значения a i обычно записываются в правом столбце платежной матрицы (см. рис. 1.1). Очевидно, что желающий перестраховаться игрок A должен предпочесть другим стратегиям ту, для которой гарантированный выигрыш a i максимален.
Обозначим это максимальное значение 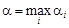 . Величина
. Величина 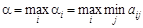 есть гарантированный выигрыш, который игрок A может получить в игре, и называется нижней ценой игры или максимином. Стратегия, обеспечивающая игроку A получение нижней цены игры, называется максиминной стратегией.
есть гарантированный выигрыш, который игрок A может получить в игре, и называется нижней ценой игры или максимином. Стратегия, обеспечивающая игроку A получение нижней цены игры, называется максиминной стратегией.
Аналогичные рассуждения могут быть проведены по поводу действий игрока В. С его точки зрения, в платежной матрице приведены проигрыши. В каждом из столбцов он должен найти максимальное значение проигрыша при выборе стратегии B j:
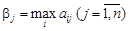 .
.
Значения b j записываются в дополнительной строке платежной матрицы (см. рис. 1.1).
Выбирать стратегию игроку B следует так, чтобы минимизировать величину проигрыша при любых действиях соперника, т. е. обеспечить 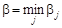 . Величина
. Величина 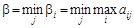 называется верхней ценой игры (минимаксом), а соответствующая ей чистая стратегия B j – минимаксной.
называется верхней ценой игры (минимаксом), а соответствующая ей чистая стратегия B j – минимаксной.
Можно показать, что максимин не превосходит минимакс, т. е. a £ b. Если в игре нижняя цена равна верхней (a = b), то говорят, что игра имеет седловую точку и чистую цену игры g = a = b. Пару чистых стратегий (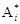 ,
, 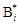 ), соотвествующих g, называют седловой точкой матричной игры, а элемент aij *платежной матрицы, стоящий на пересечении i *-й строки и j *-го столбца, – седловым элементом платежной матрицы. Он одновременно является минимальным в своей строке и максимальным в своем столбце. Стратегии
), соотвествующих g, называют седловой точкой матричной игры, а элемент aij *платежной матрицы, стоящий на пересечении i *-й строки и j *-го столбца, – седловым элементом платежной матрицы. Он одновременно является минимальным в своей строке и максимальным в своем столбце. Стратегии 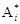 и
и 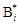 , образующие седловую точку, являются оптимальными. Значения
, образующие седловую точку, являются оптимальными. Значения 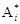 ;
; 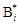 ;g называют решением игры.
;g называют решением игры.
Пример. В игре принимают участие два игрока. Каждый из игроков может записать независимо от другого цифру 4, 5 или 6. Если разность между цифрами, записанными игроками А и В положительна, то игрок А выигрывает количество очков, равное этой разности. Если разность отрицательна, то выигрывает игрок В. Если разность равна нулю, то игра заканчивается вничью. Составить платежную матрицу и найти решение игры.
Решение. Составим платежную матрицу игры. Чистыми стратегиями игрока А будут: А1 – записать число 4; А2 – записать число 5; А3 – записать число 6. У игрока В чистыми будут аналогичные стратегии. Элемент матрицы а11 = 0, так как в ситуации (А1; В1) оба игрока записывают цифру 4 и выигрыш игрока А равен 4 – 4 = 0. В ситуации (А1; В2) выигрыш игрока А составит а12 = 4–5 = –1. Аналогичным образом вычисляются остальные элементы платежной матрицы (рис. 1.2).
| B1 (4) | B2 (5) | B3 (6) | a i | |
| A1 (4) | –1 | –2 | –2 | |
| A2 (5) | –1 | –1 | ||
| A3 (6) | 0* | |||
| b j |
Рис. 1.2. Платежная матрица примера
Определим минимальные гарантированные выигрыши игрока А, равные 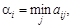 при выборе им стратегий А i. Так, если игрок А записал цифру 4, то его минимальный выигрыш при выборе данной стратегии составит a1 = min(0; –1; –2) = –2. Аналогично находим a2 = min(1; 0; –1)= –1, если игрок А записал цифру 5 и a3 =
при выборе им стратегий А i. Так, если игрок А записал цифру 4, то его минимальный выигрыш при выборе данной стратегии составит a1 = min(0; –1; –2) = –2. Аналогично находим a2 = min(1; 0; –1)= –1, если игрок А записал цифру 5 и a3 =
= min(2; 1; 0) = 0, если им записана цифра 6. Найдем нижнюю цену игры игрока А, воспользовавшись “принципом максимина”, т. е. 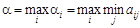 . Нижняя цена игры для игрока А составит
. Нижняя цена игры для игрока А составит
a = max(–2; –1; 0) = 0. Таким образом, максиминному выбору игрока А будет отвечать третья стратегия, гарантирующая выигрыш, равный нулю.
Для игрока В значения элементов 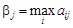 составят соответственно
составят соответственно 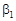 = 2,
= 2, 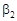 = 1,
= 1, 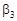 = 0. Верхняя чистая цена игры для игрока В по “принципу минимакса” составит
= 0. Верхняя чистая цена игры для игрока В по “принципу минимакса” составит 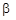 = min (2; 1; 0) = 0. Следовательно, минимаксному выбору игрока В будет отвечать третья стратегия, гарантирующая минимальный проигрыш, равный нулю.
= min (2; 1; 0) = 0. Следовательно, минимаксному выбору игрока В будет отвечать третья стратегия, гарантирующая минимальный проигрыш, равный нулю.
Так как a = b, то данная игра имеет седловую точку, т. е. третья чистая стратегия игрока А и третья чистая стратегия игрока В образуют седловую точку со значением 0 и данная матричная игра имеет решение (A3; B3; 0).
Date: 2015-07-25; view: 569; Нарушение авторских прав