Решение матричных игр без седловых точек

Если матрица игры содержит седловую точку, то ее решение находится по принципу минимакса (матричная игра решается в чистых стратегиях). Если же платежная матрица не имеет седловой точки, т. е. a < b, то решением для каждого игрока будет сложная стратегия, состоящая в случайном применении им двух и более чистых стратегий.

Если в процессе игры игрок применяет попеременно несколько чистых стратегий с определенными частотами, то такая стратегия игрока называется смешанной.

Однако, следует отметить, что применение игроками смешанных стратегий имеет смысл только тогда, когда данная игра проводится ими многократно. В случае однократно проводимой игры, не имеющей седловой точки, дать какие-либо содержательные рекомендации игрокам не представляется возможным.

Смешанной стратегией игрока А называется вектор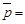
= (p ₁; p ₂; …, p_m), где p_i – вероятность, с которой игрок A выбирает свою чистую стратегию A _i. Компоненты вектора р удовлетворяют условиям: .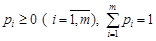

Смешанной стратегией игрока B называют вектор 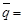, где q_i – вероятность применения игроком B его чистой стратегии B _j. При этом .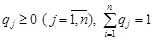

Решить задачу в смешанных стратегиях означает найти такие оптимальные смешанные стратеги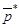и и , которые доставляют игроку A максимальный средний выигрыш, а игроку B – минимальный средний проигрыш.

Ценой игры g при решении в смешанных стратегиях называется величина среднего выигрыша игрока A (среднего проигрыша B), приходящегося на одну партию. Стратегии игроков, входящие в их оптимальные смешанные стратегии, называются активными.

Можно показать, что цена игры всегда удовлетворяет условию:

.

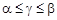Следовательно, если каждый игрок придерживается своих смешанных стратегий при многократном повторении игры, то он получает более выгодный для себя результат, чем применяя “перестраховочные” стратегии, соответствующие a и b. Каждый из игроков не заинтересован в отходе от своей оптимальной стратегии, так как ему это невыгодно.

1.1.5. Решение матричной игры путем сведения
к задаче линейного программирования

Пусть платежная матрица игры не содержит седловой точки, следовательно, игра решается в смешанных стратегиях.

Будем считать, что все элементы платежной матрицы неотрицательны (если это не так, то можно воспользоваться правилом перевода элементов матрицы в область неотрицательных значений (см.
п. 1.3). Следовательно, можно принять, что g > 0.

Применение игроком А оптимальной смешанной стратегии 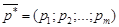гарантирует ему, независимо от поведения игрока В, выигрыш, не меньший цены игры g.

Если игрок А применяет свою оптимальную стратегию 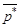, а игрок В свою чистую стратегию В _j, то средний выигрыш игрока А будет равен:

.

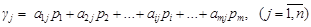Учитывая, что g _j не может быть меньше g, можем записать условие:

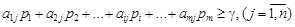. (1.5)

Разделив левую и правую части неравенства (1.5) на цену игры
g > 0, получим:

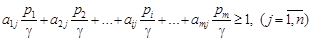. (1.6)

Введем новые обозначения:

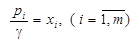. (1.7)

Тогда неравенства (1.6) запишутся в виде:

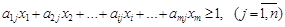. (1.8)

где x_i 0, так как p_i 0, g > 0.

Компоненты вектора р удовлетворяют следующему условию:

p ₁ + p ₂ + … + p_m = 1.

Учитывая соотношение (1.7) получим, что переменные x_i удовлетворяют условию:

.

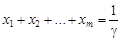Учитывая, что игрок А стремится максимизировать g, получаем линейную функцию

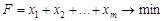. (1.9)

Таким образом, приходим к следующей задаче линейного программирования: найти неотрицательные значения переменных x_i (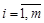), минимизирующие линейную функцию (1.9) и удовлетворяющие ограничениям (1.8):

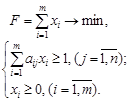
Решив данную задачу, найдем цену игры 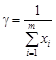и вероятность применения игроком А его чистых стратегий .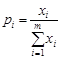

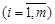Аналогично для игрока В нужно решить двойственную задачу:

,

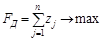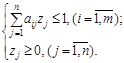
Решив двойственную задачу, найдем вероятности применения игроком В его чистых стратегий из выражения:

.

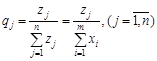Date: 2015-07-25; view: 858; Нарушение авторских прав