Модель идеального вытеснения

Модель идеального вытеснения относится к классу моделей с распределенными параметрами. Для таких моделей характерно, что переменные процесса могут изменяться как во времени, так и в пространстве, а также могут изменяться только в пространстве. Их математическое описание включает обычно дифференциальные уравнения в частных производных, либо обыкновенные дифференциальные уравнения в случае стационарных процессов с одной пространственной переменной. Примером процесса, описываемого такими моделями, служит трубчатый аппарат с большим отношением длины к диаметру и значительной скоростью движения реагентов (рис.2).

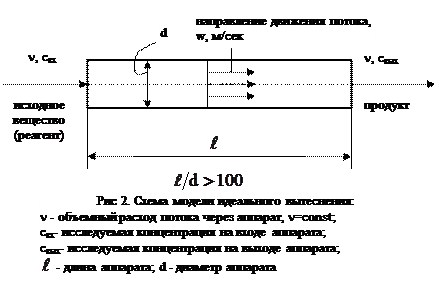В основе модели идеального вытеснения лежит допущение о поршневом течении, без перемешивания вдоль потока при равномерном распределении вещества в направлении, перпендикулярном движению потока. Время пребывания всех частиц в системе одинаково и равно отношению объема системы (аппарата) к объемному расходу жидкости. Такой поток, например, имеет место в трубчатом аппарате при турбулентном режиме течения жидкости через него.

Математическое описание модели идеального вытеснения (рис. 2) имеет вид:

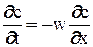, (4)

где t - исследуемый интервал времени; x - координата, вдоль которой передвигается вещество, и вдоль которой исследуется изменение концентрации; w - линейная скорость передвижения вещества (м/сек), 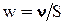, где S - площадь сечения аппарата.

Для решения дифференциального уравнения в частных производных (4) начальное условие: в начальный (нулевой) момент времени по всей длине аппарата начальная концентрация была равна некоторому начальному значению c_н, т.е.

с(0, x) = c_н(x), при t = 0, 0 < x < 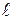, (5)

граничное условие: концентрация в начале аппарата в любой момент времени есть некоторая входная функция от времени, т.е.

с(t, 0) = c_вх(t), при x = 0, t > 0. (6)

Решение уравнения (4), удовлетворяющее условиям (5) и (6), имеет вид:

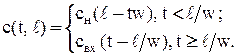(7)

Из решения (7) следует, что любое изменение концентрации на входе в аппарате идеального вытеснения появляется на его выходе через время, равное среднему времени пребывания 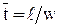, где 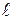- длина аппарата (рис. 2).

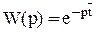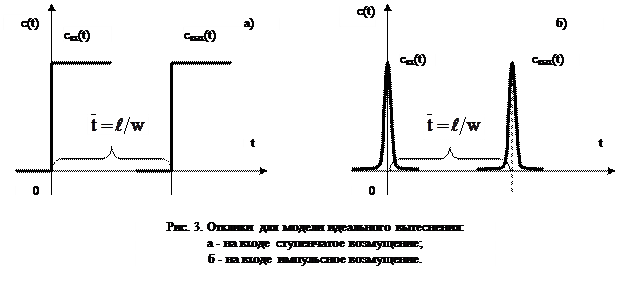
Аппарат идеального вытеснения аппроксимируют звеном чистого запаздывания. Передаточная функция этого звена имеет вид , где 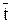- время транспортного запаздывания. Виды выходных сигналов при различных входных воздействиях представлены на рис. 3.

Date: 2015-07-24; view: 907; Нарушение авторских прав