
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

ЛЕКЦИЯ № 3
|
|
Пример. Составить математическое описание следующей задачи об оптимальном составе сплава и представить полученную задачу линейного программирования в каноническом виде.
Для приготовления b0 кг сплава с заданными свойствами используют вещества Аj, j = 1`,n. В x кг вещества Аj содержится аijх кг химического элемента Вi, i = 1`,m. Содержание элемента Вi в сплаве должно заключиться в пределах от bi до bi кг. Стоимость одного кг вещества Аj составляет Сj руб. Требуется определить такой состав для приготовления сплава, при котором общая стоимость израсходованных веществ минимальна.
Решение.
Обозначим хj количество кг вещества Аj, используемое для приготовления сплава (очевидно хj ³ 0, j = 1`,n). Тогда содержание элемента Вi в сплаве составит 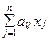 кг, а стоимость израсходованных веществ будет равна
кг, а стоимость израсходованных веществ будет равна 

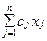 руб.
руб.
Поэтому с учетом ограничений на содержание элементов Вi в сплаве, для величин хj получим следующие неравенства 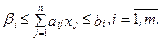
Кроме того, количество сплава должно составлять b0 кг, поэтому 
Таким образом математическое описание задачи об оптимальном составе сплава принимает вид
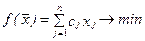 (6)
(6)
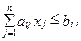 (7)
(7)
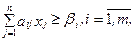 (8)
(8)
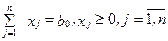 (9)
(9)
Запишем эту задачу линейного программирования в каноническом виде.
Среди ограничений (7) – (9) на переменные хj содержится 2m неравенств (7), (8). Для преобразования их в ограничения-равенства введём 2m дополнительных неотрицательных переменных хn+i и хn+m+i, i = 1,m.
Прибавив переменные хn+i к левым частям соответствующих неравенств (7) и вычтя переменные хn+m+i из левых частей неравенств (8), получим задачу линейного программирования в каноническом виде.
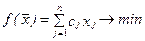
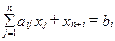
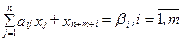

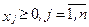
Date: 2015-07-24; view: 589; Нарушение авторских прав