
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Линейного программирования
|
|
Общим методом решения произвольной задачи линейного программирования является симплекс-метод.
Выберем какой-нибудь базисный минор матрицы А. Для определённости будем считать, что он соответствует первым Г столбцам и строкам этой матрицы. Если Г<m, то уравнения с номерами i = Г+1,..., m, являющиеся следствием остальных уравнений системы, отбросим, в дальнейшем Г=m.
Для решения системы уравнений относительно базисных переменных xj, j=1,..., m, с помощью преобразований приведём её к виду:
x1 + a(0)1,m+1xm+1+...+a(0)1,nxn = b1(0),
x2 + a(0)2,m+1xm+1+...+a(0)2,nxn = b2(0),
.................................................................. (1)
xm + a(0)m,m+1xm+1+...+a(0)m,nxn = bm(0),
тогда общее решение системы запишется:
x1 = b1(0) - a(0)1,m+1xm+1 -...- a(0)1,nxn,
x2 = b2(0) - a(0)2,m+1xm+1 -...- a(0)2,nxn,
................................................................. (2)
xm = bm(0) - a(0)m,m+1xm+1 -...- a(0)m,nxn,
где свободные переменные xm+1,..., xn могут принимать произвольные значения.
Положив их равными нулю, получим частное решение:
x1 = b1(0), x2 = b2(0),..., xm = bm(0), xm+1 = xm+2 =...= xn = 0 или
x(0) = (b1(0), b2(0),..., bm(0), 0, 0,...,0). (3)
которое назовем базисным решением системы ограничений. Каждому выбору базисных переменных соответствует своё базисное решение. Если все компоненты базисного решения (3) удовлетворяют условию неотрицательности, т.е.
bi(0) ³ 0, i = 1,...,m,
то такое решение называют допустимым базисным решением или угловой точкой допустимого множества D задачи линейного программирования. Если среди неотрицательных чисел bi(0) в (3) есть равные 0, то допустимое базисное решение называют вырожденным (вырожденной угловой точкой), а соответствующая задача линейного программирования также называется вырожденной.
В основе симплекс-метода лежит следующий факт:
Если задача линейного программирования разрешима, то минимум целевой функции f(`x) достигается хотя бы в одной из угловых точек допустимого множества D этой задачи.
Так как различные базисные решения соответствуют различным вариантам выбора m базисных из общего числа n переменных xj, то чиcло допустимых базисных решений (угловых точек) не превышает Cnm. Поэтому задачу линейного программирования можно решеть посредством перебора конечного числа угловых точек допустимого множества D, сравнивая значения целевой функции в этих точках. Однако при большой размерности n задачи линейного программирования этот подход затруднителен. Идея симплекс-метода состоит в направленном переборе угловых точек допустимого множества D с последовательным уменьшением целевой функции f(`x).
ОПИСАНИЕ СИМПЛЕКС - МЕТОДА
Предположим, что задача линейного программирования является невырожденной, а базисное решение допустимым. Используя соотношение (2), выразим целевую функцию через свободные переменные xj, j = m+1,..., n


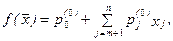 (4)
(4)
где 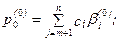
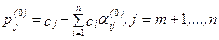
Справедливы следующие утверждения:
а) если в выражении (4) все коэффициенты pj(0), j = m+1,..., n
неотрицательны, то в угловой точке (3) достигается минимум целевой функции f(`x) на допустимом множестве D и этот минимум равен p0(0);
б) если среди отрицательных коэффициентов pj(0), j ¹ 0, из (4) есть такой (например pa(0)), что в (1) все коэффициенты ail(0) £ 0, i = 1,..., m, то целевая функция f(`x) не ограничена снизу на допустимом множестве D и задача не имеет решений.
в) если хотя бы один из коэффициентов pj(0), j ¹ 0, из (4) отрицателен (например, pl(0) < 0) и при этом среди коэффициентов ail(0) в (1) есть хотя бы один положительный, то существует угловая точка `x(1) множества D такая, что f(`x(1)) < f(`x(0)).
В случаях а) и б) процесс решения задачи линейного программирования на этом заканчивается. Рассмотрим подробнее случай в). Пусть в (4) коэффициент pl(0) < 0 и в (1) имеются положительные коэффициенты ail(0). Найдём номер k базисной переменной из условия.
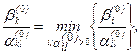 (5)
(5)
где минимум берётся по всем номерам i = 1,..., m, для которых ail(0) > 0.
Найдём решение системы ограничений, считая свободными переменные xm+1,..., xl-1,..., xk, xl+1,..., xn, т.е. поменяв местами свободную переменную xl с базисной переменной xk. Система уравнений (1) в этом случае запишется следующим образом:
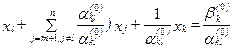 |
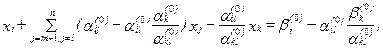 i = 1,..., m, i ¹ k (6)
i = 1,..., m, i ¹ k (6)
а зависимость целевой функции от новых свободных переменных примет вид
 (7)
(7)
Компоненты нового базисного решения `x(1) можно найти, приравняв нулю свободные переменные xj, j = m+1,..., n, j ¹ l и xk, и найдя при этом условии значения базисных переменных из (6). Базисное решение`x(1) является допустимым, т.е. угловой точкой множества D, причём f(`x(1)) < f(`x(0)).
По знакам коэффициентов в системе (6) и выражении для целевой функции (7) можно сделать одно из трёх приведённых выше заключений, как это было сделано для угловой точки `x(0). В случае в) следует совершить переход к очередной угловой точке `x(2), аналогичный переходу от `x(0) к`x(1), и т.д.
Так как число угловых точек допустимого множества D не превышает Cnm, то случай в) может повторяться конечное число раз, т.е. в результате конечного числа шагов перехода к новой угловой точке будет либо найдено решение задачи, либо сделано заключение о том, что она не имеет решения.
Реализация описанного выше симплекс-метода значительно упрощается при использовании симплекс-таблиц. Записав коэффициенты уравнений (1) и целевой функции (4) соответствующим образом, получим симплекс-таблицу задачи:
| xm+1... xl... xn | ||
| x1 . . . xk . . . xm | a(0)1,m+1 ... a(0)1,1 ... a(0)1,n . . . a(0)k,m+1 ... a(0)k,1 ... a(0)k,n . . . a(0)m,m+1 ... a(0)m,1 ... a(0)m,n | b(0)1 . . . b(0)k . . . b(0)k |
| p(0)m+1 ... p(0)1 ... p(0)n | - p(0)0 |
Рассмотрим переход от симплекс-таблицы, соответствующей угловой точке x(0), к симплекс-таблице для угловой точки `x(1).
Пусть номера k и l определены так, как это сделано выше. Элемент a(0)k,1, а также строка и столбец на пересечении которых он стоит, называется разрешающими или опорными. Из формул (6) и (7) следует, что преобразование исходной симплекс-таблицы с опорным элементом a(0)k,1 приводит к новой симплекс-таблице, для определения элементов которой необходимо выполнить следующие опреации:
1) Поменять местами переменные xk и xl, остальные переменные оставить на прежних местах.
2) На место опорного элемента поставить число 1/a(0)k,1.
3) На остальных местах разрешающей строки записать соответствующие элементы исходной таблицы, делённые на опорный элемент.
4) На свободные места разрешающего столбца поставить со знаком минус соответствующие элементы исходной таблицы, делённые на опорный элемент.
5) Оставшиеся свободные места в новой симплекс таблице заполнить построчно следующим образом: из строки элементов исходной таблицы вычесть произведение и элемента из разрешающего столбца на уже заполненную разрешающую строку новой таблицы.
Пример. Решить задачу симплекс методом:
f(`x) = x1+ 9x2 +5 x3 +3x4 + 4x5+ 14x6 ® min
x1 + x4 = 20
x2 + x5 = 50
x3 + x6 =30
x4 + x5+ x6=60
xj ³0, j = 1,..., 6.
Столбцы 2, 4, 5 и 6 матрицы А образуют базисный минор. С помощью эквивалентных преобразований приводим эту систему к виду (1), где базисными являются переменные x2, x4, x5, x6.
x2 + x1 + x3 = 40 (8)
x4 + x1 = 20
x5 - x1 – x3 = 10
x6 + x3 = 30
Исключив с помощью (8) базисные переменные в выражении для целевой функции, получим:
f(`x) = 880 - 7x1 - 14x3 (9)
| x1 x3 | ||
| x2 x4 x5 x6 | 1 1 1 0 -1 -1 0 1 | |
| -7 -14 | -880 |
Так как min (40/1; 30/1) = 30/1, то разрешающей является строка, соответствующая базисной переменной x6.
| x1 x6 | x2 x6 | ||||
| x2 x4 x5 x3 | 1 -1 1 0 -1 1 0 1 | x1 x4 x5 x3 | 1 -1 -1 1 1 0 0 1 | ||
| -7 14 | -460 | 7 7 | -390 |
Ответ: `x* = `x(2) = (10; 0; 30; 10; 50; 0). f* = 390.
ЛЕКЦИЯ №4.
ТИПОВЫЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
ЗАДАЧА ПЛАНИРОВЫАНИЯ ПРИ ОГРАНИЧЕНИЯХ НА РЕСУРСЫ
Задача. У предприятия есть m видов ресурсов (сырье, оборудование, рабочая сила и т.д), каждый в количестве bi единиц, i=1,2,…,m. Предприятие выпускает n видов продукции, aij – количество единиц i-того вида ресурса, необходимого для выпуска единицы j-той продукции. Прибыль от одной единицы j-той продукции равна Сj,$, а затраты на ее выпуск - Sj, $. Продукции j-того вида надо выпустить не менее Pj единиц. Единица j-той продукции содержит Vkj единиц k-го потребительского свойства (калорийность или содержание определенных питательных веществ в производимых продуктах питания, производительность выпускаемых средств и т.д), которого во всей выпускаемой продукции должно быть не менее rk единиц, k=1,2,…,l. Определить количество выпускаемой продукции каждого вида, при котором суммарная прибыль максимальна либо минимальны затраты.
Решение. Следует помнить, что при составлении любой, не только линейной, модели параметрической оптимизации необходимо выполнить три этапа:
1) Определить, значения каких параметров надо найти (что является входными параметрами) и обозначить их через х1, х2,…, хn.
2) Записать выражение для целевой функции через х1, х2,…, хn.
3) Записать выражения для ограничений через х1, х2,…, хn.
Для задачи планирования имеем:
1) Обозначим хj – объем выпуска j-той продукции (j=1,2,…,n).
2) Целевая функция – прибыль или затраты. От одной единицы 1-ой продукции прибыль составит С1, $, а от х1 единиц – C1x1, $. Аналогично, для всех видов продукции суммарная прибыль составит:
Q1=C1x1+C2x2+…+Cnxn→max (1)
Суммарные затраты:
Q2=S1x1+S2x2+…+Snxn→min. (1*)
3) Ограничения:
Ограничения на объем выпуска: согласно условию задачи xj≥Pj.
Ограничения на ресурсы: на одну единицу 1-ой продукции надо затратить a11
Date: 2015-07-24; view: 483; Нарушение авторских прав