Пример 2.2. Моделирование реактора идеального вытеснения

Для получения уравнений математической модели рассмотрим реактор идеального вытеснения, в котором проводится изотермическая реакция первого порядка А → Р → S.

Идеализированная схема реактора представлена на рис. 2.6. Условия физической реализуемости этой модели выполняются в случае поршневого потока, когда предполагается, что в направлении его движения смешение полностью отсутствует, а в направлении, перпендикулярном движению, происходит идеальное смешение.

V - объем реактора, м³; S - площадь поперечного сечения реактора, м²; L - длина реактора, м; υ - объемный расход, м³/ч; и = υ /S- линейная скорость потока, м/ч;

τ= l/и- время пребывания, ч

Рис. 2.6

Уравнение, описывающее изменение концентрации вещества А в зоне вытеснения при стационарном режиме будет иметь вид:

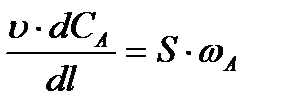(2.8)

При моделировании реакторов удобнее перейти от переменной интегрирования длины l к переменной τ - время пребывания, поскольку они связаны известным соотношением:

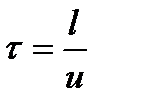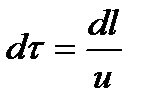или или 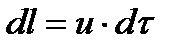(2.9)

Сечение зоны вытеснения можно выразить через объемную и линейную скорость потока:

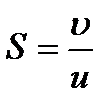(2.10)

Тогда выражение (2.8) можно записать так:

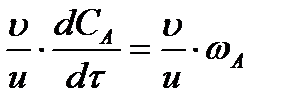или (2.11)

Математическое описание реактора идеального вытеснения в стационарном режиме совпадает с известным кинетическим уравнением, приводящимся иногда как определение скорости химической реакции. Переменная τ имеет размерность времени и обозначает время пребывания элементарного объема реагирующей смеси в зоне реакции. Поэтому это уравнение можно рассматривать так же как описание реактора идеального смешения периодического действия, в котором процесс проводится до определенного момента времени при отсутствии подачи исходных реагентов в аппарат и отвода из него продуктов реакции.

На основании стехиометрии реакции А → Р → S, можно записать уравнения, описывающие изменение концентраций веществ в реакторе идеального вытеснения по времени пребывания:

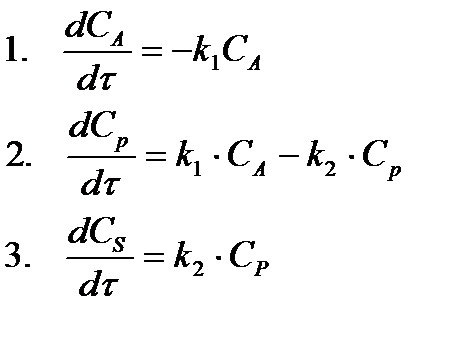(2.12)

Граничные условия интегрирования:

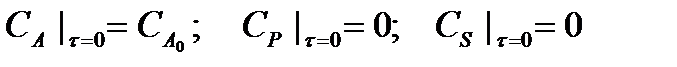(2.13)

Система дифференциальных уравнений (2.12) может быть решена аналитически и численными методами.

Рассмотрим аналитическое решение.

Первое дифференциальное уравнение по веществу А с разделяющимися переменными интегрируем следующим образом:

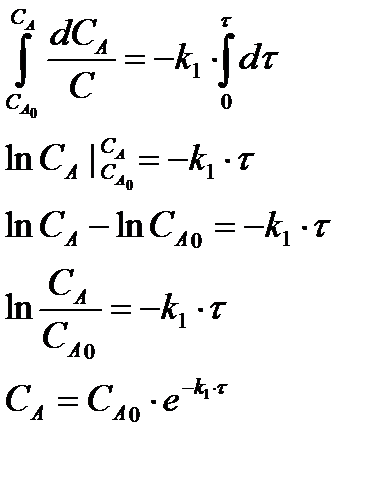(2.14)

Второе дифференциальное уравнение по веществу Р интегрируется достаточно сложным методом вариации произвольных постоянных. В результате интегрирования получено выражение

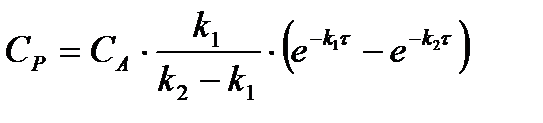(2.15)

Зависимость концентрации вещества S от времени пребывания может быть получена из уравнения материального баланса:

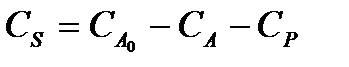(2.16)

Функция С_р(τ) имеет максимум. Величину τ_опт, соответствующую максимальному значению концентрации С_р, можно найти аналитически.

Дифференцированием второго уравнения системы (2.15) по τ находим оптимальные условия проведения реакции:

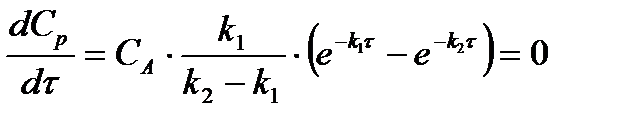(2.17)

Анализ уравнения (2.17) показывает, что если С_А ≠ 0; k₁ ≠ k₂;

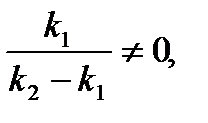выражение (2.17) можно упростить:

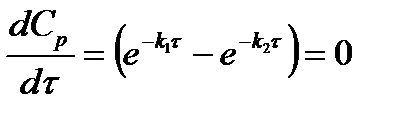(2.18)

При дифференцировании выражения (2.18) получим:

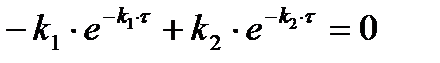(2.19)

После логарифмирования выражения (2.19) получим:

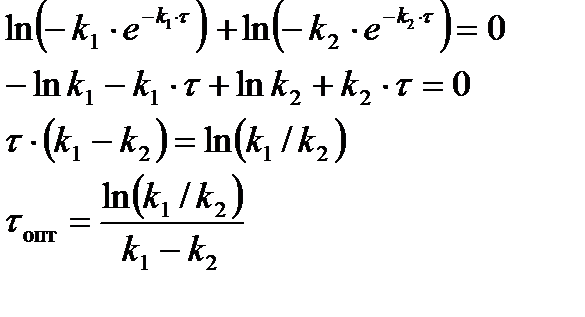(2.20)

Date: 2015-07-24; view: 1186; Нарушение авторских прав