
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Найти матрицу в базисе из собственных векторов
|
|
Если собственные векторы матрицы 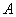 образуют базис, то она представима в виде:
образуют базис, то она представима в виде:
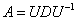 , где
, где  – матрица составленная из координат собственных векторов,
– матрица составленная из координат собственных векторов,  – диагональная матрица из собственных чисел.
– диагональная матрица из собственных чисел.
Такое разложение матрицы также называют каноническим или диагональным.
Рассмотрим матрицу 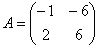 первого примера. Её собственные векторы
первого примера. Её собственные векторы 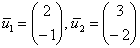 линейно независимы и образуют базис. Составим матрицу из их координат:
линейно независимы и образуют базис. Составим матрицу из их координат:
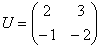
На главной диагонали матрицы  в соответствующем порядке располагаются собственные числа, а остальные элементы равняются нулю:
в соответствующем порядке располагаются собственные числа, а остальные элементы равняются нулю:
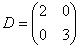
Подчёркиваю важность порядка: перестановка «двойки» и «тройки» недопустима! Точнее, переставить числа можно: 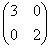 , но тогда и в матрице
, но тогда и в матрице  следует поменять местами собственные векторы:
следует поменять местами собственные векторы: 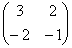 .
.
По обычному алгоритму нахождения обратной матрицы либо методом Жордано-Гаусса нетрудно получить 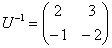 . Это не опечатка – перед вами редкое, как солнечное затмение событие, когда обратная совпала с исходной матрицей.
. Это не опечатка – перед вами редкое, как солнечное затмение событие, когда обратная совпала с исходной матрицей.
Таким образом, матрица 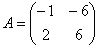 запишется в следующем виде:
запишется в следующем виде:

Желающие могут перемножить три матрицы и удостовериться, что произведение равно 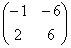 .
.
Каноническое разложение матрицы бывает удобно использовать в ряде задач, поскольку оно значительно упрощает некоторые матричные операции.
Пример 3
Записать матрицу в базисе из собственных векторов
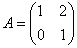
Решение: найдем собственные значения. Составим и решим характеристическое уравнение:
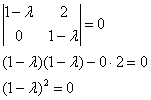
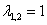 – получены кратные собственные числа.
– получены кратные собственные числа.
Мысленно либо на черновике подставим 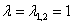 в определитель
в определитель 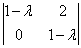 и запишем однородную систему линейных уравнений:
и запишем однородную систему линейных уравнений:
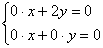
Вторая координата принудительно равна нулю: 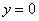 (иначе в первом уравнении получится неверное равенство). За «икс» можно принять любое ненулевое значение, в хорошем стиле положим, что
(иначе в первом уравнении получится неверное равенство). За «икс» можно принять любое ненулевое значение, в хорошем стиле положим, что 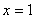 .
.
Таким образом, кратным собственным числам соответствует единственный собственный вектор 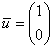 .
.
! Примечание: в общем случае такое утверждение неверно!
Канонические разложение матрицы имеет вид 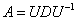 , и в нашей ситуации данного разложения не существует. Почему? Потому что невозможно записать матрицу
, и в нашей ситуации данного разложения не существует. Почему? Потому что невозможно записать матрицу  , которая должна состоять из двух линейно независимых собственных векторов. Размерность вектора равна двум («икс» и «игрек»), но сам-то вектор – один-одинёшенек. Коллинеарный товарищ, например
, которая должна состоять из двух линейно независимых собственных векторов. Размерность вектора равна двум («икс» и «игрек»), но сам-то вектор – один-одинёшенек. Коллинеарный товарищ, например 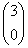 , в пару не годится (хотя бы по той причине, что
, в пару не годится (хотя бы по той причине, что 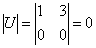 и обратной матрицы
и обратной матрицы 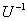 попросту не существует).
попросту не существует).
Ответ: собственные векторы не образуют базиса, поэтому требуемое разложение неосуществимо.
Обратите внимание на корректность и точность ответа – нас никто не спрашивал о собственных значениях и собственных векторах.
Задача с матрицей «три на три» отличаются бОльшей технической сложностью:
Пример 4
Найти собственные векторы линейного преобразования, заданного матрицей
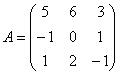
Решение: немного другая формулировка задачи смущать не должна – генеральная линия партии остаётся прежней. Энтузиасты могут провести самостоятельные выкладки по аналогии с Примером №1, я же ограничусь «рабочим» решением примера.
По условию требуется найти собственные векторы, но алгоритм таков, что в первую очередь всё равно нужно найти собственные числа.
Вычтем «лямбду» из всех чисел главной диагонали матрицы 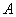 и составим её характеристическое уравнение:
и составим её характеристическое уравнение:
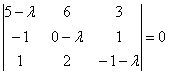
Определитель раскроем по первому столбцу:
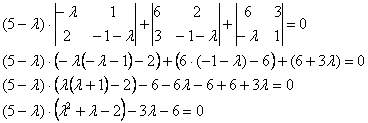
На этом месте немного притормозим и познакомимся с очень полезным техническим приёмом, который значительно упростит дальнейшую жизнь. Практически во всех методических пособиях вам будет предложено раскрыть все скобки, получить слева многочлен 3-ей степени, затем подбором найти корень и стать жертвой долгих мытарств, описанных в Примере №1 урока Сложные пределы. За годы практики я отработал рациональную схему, позволяющую избежать этих неприятностей:
Сначала представим в виде произведения «хвост» левой части:
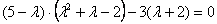
Выполненное действие не привело к заметному результату.
Поэтому пробуем разложить на множители квадратный трёхчлен 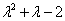 . Решив квадратное уравнение, получаем
. Решив квадратное уравнение, получаем 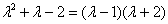 .
.
Таким образом:
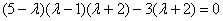
Вынесем 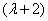 за скобку и проведём дальнейшие упрощения:
за скобку и проведём дальнейшие упрощения:
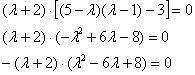
Решаем ещё одно квадратное уравнение, в итоге:
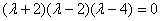
Это была самая длинная ветка алгоритма, в большинстве случаев произведение получается значительно быстрее.
Собственные значения всегда стараемся расположить в порядке возрастания:
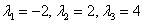
Найдем собственные векторы:
1) Мысленно либо на черновике подставим значение 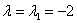 в определитель
в определитель 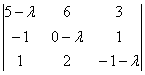 , с которого «снимем» коэффициенты однородной системы:
, с которого «снимем» коэффициенты однородной системы:
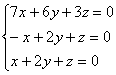
Систему можно решить с помощью элементарных преобразований и в следующих примерах мы прибегнем к данному методу. Но здесь гораздо быстрее срабатывает «школьный» способ. Из 3-го уравнения выразим: 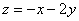 – подставим во второе уравнение:
– подставим во второе уравнение:
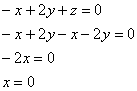
Поскольку первая координата нулевая, то получаем систему 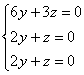 , из каждого уравнения которой следует, что
, из каждого уравнения которой следует, что 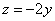 .
.
И снова обратите внимание на обязательное наличие линейной зависимости. Если получается только тривиальное решение 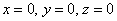 , то либо неверно найдено собственное число, либо с ошибкой составлена/решена система.
, то либо неверно найдено собственное число, либо с ошибкой составлена/решена система.
Компактные координаты даёт значение 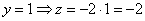
Собственный вектор: 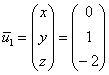
Крайне желательно проверить, что найденное решение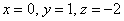 удовлетворяет каждому уравнению системы. В последующих пунктах и в последующих задачах рекомендую принять данное пожелание за обязательное правило.
удовлетворяет каждому уравнению системы. В последующих пунктах и в последующих задачах рекомендую принять данное пожелание за обязательное правило.
2) Для собственного значения 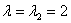 по такому же принципу получаем следующую систему:
по такому же принципу получаем следующую систему:
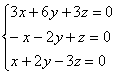
Из 2-го уравнения системы выразим: 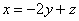 – подставим в третье уравнение:
– подставим в третье уравнение:
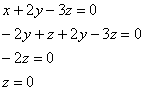
Поскольку «зетовая» координата равна нулю, то получаем систему 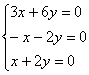 , из каждого уравнения которой следует линейная зависимость
, из каждого уравнения которой следует линейная зависимость 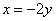 .
.
Пусть 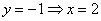
Проверяем, что решение 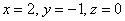 удовлетворяет каждому уравнению системы.
удовлетворяет каждому уравнению системы.
Таким образом, собственный вектор: 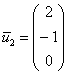 .
.
3) И, наконец, собственному значению 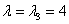 соответствует система:
соответствует система:
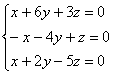
Второе уравнение выглядит самым простым, поэтому из него выразим 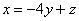 и подставим в 1-ое и 3-е уравнение:
и подставим в 1-ое и 3-е уравнение:
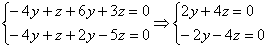
Всё хорошо – выявилась линейная зависимость  , которую подставляем в выражение
, которую подставляем в выражение 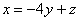 :
:
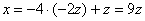
В результате «икс» и «игрек» оказались выражены через «зет»: 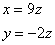 . На практике не обязательно добиваться именно таких взаимосвязей, в некоторых случаях удобнее выразить
. На практике не обязательно добиваться именно таких взаимосвязей, в некоторых случаях удобнее выразить 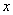 и
и 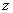 через
через 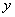 либо
либо 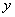 и
и 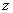 через
через 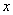 . Или даже «паровозиком» – например, «икс» через «игрек», а «игрек» через «зет»
. Или даже «паровозиком» – например, «икс» через «игрек», а «игрек» через «зет»
Положим 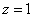 , тогда:
, тогда:
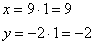
Проверяем, что найденное решение 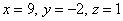 удовлетворяет каждому уравнению системы и записываем третий собственный вектор
удовлетворяет каждому уравнению системы и записываем третий собственный вектор 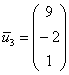
Ответ: собственные векторы: 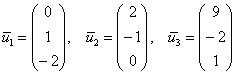
Если бы по условию требовалось найти каноническое разложение 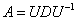 – то здесь это возможно. Различным собственным числам соответствуют разные линейно независимые собственные векторы: составляем матрицу
– то здесь это возможно. Различным собственным числам соответствуют разные линейно независимые собственные векторы: составляем матрицу 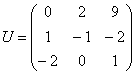 из их координат, диагональную матрицу
из их координат, диагональную матрицу 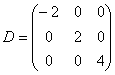 из соответствующих собственных значений и находим обратную матрицу
из соответствующих собственных значений и находим обратную матрицу 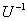 .
.
Задача с более простыми вычислениями для самостоятельного решения:
Пример 5
Найти собственные векторы линейного преобразования, заданного матрицей
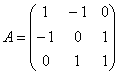
При нахождении собственных чисел постарайтесь не доводить дело до многочлена 3-ей степени. Кроме того, ваши решения систем могут отличаться от моих решений – здесь нет однозначности; и векторы, которые вы найдёте, могут отличаться от векторов образца с точностью до пропорциональности их соответствующих координат. Например, 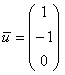 и
и  . Эстетичнее представить ответ в виде
. Эстетичнее представить ответ в виде 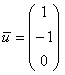 , но ничего страшного, если остановитесь и на втором варианте. Однако всему есть разумные пределы, версия
, но ничего страшного, если остановитесь и на втором варианте. Однако всему есть разумные пределы, версия 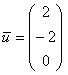 смотрится уже не очень хорошо.
смотрится уже не очень хорошо.
Примерный чистовой образец оформления задания в конце урока.
Date: 2015-07-23; view: 3685; Нарушение авторских прав