Как найти собственные значения и собственные векторы матрицы?

Проведём исследование и получим алгоритм, по которому нужно решать данную задачу. Люди, которые не очень хорошо разбираются в математике (да и которые хорошо) обычно в страхе или отвращении захлопывают учебник, когда речь заходит о каком-либо доказательстве или выводе какой-нибудь формулы. Но это не тот случай – всё будет понятно даже полному чайнику:

Пример 1

Найти собственные числа и собственные векторы матрицы

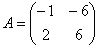
Перед вами старая знакомая матрица, у которой я уже выдал одно собственное значение и один собственный вектор. Давайте научимся добывать их самостоятельно!

Обозначим через 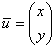неизвестный собственный вектор. Тогда матричное уравнение 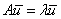запишется следующим образом:

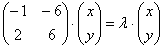
В левой части по обычному правилу проведём матричное умножение, в правой части – внесём «лямбду»:

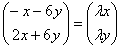
Две матрицы равны, если равны их соответствующие элементы. Приравниваем соответствующие элементы векторов-столбцов и получаем однородную систему линейных уравнений:

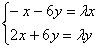
Перенесём всё налево:

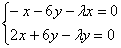
В первом уравнении за скобки вынесем «икс», во втором уравнении – «игрек»:

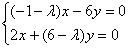
По определению, собственный вектор не может быть нулевым 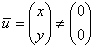, поэтому нас не устраивает тривиальное решение 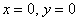системы. Следовательно, уравнения линейно зависимы иопределительматрицы системы равен нулю:

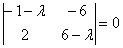
Это так называемое характеристическое уравнение матрицы 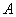, корни которого являются собственными числами данной матрицы.

Решение: на практике, как правило, не нужно расписывать подробный вывод формулы – вполне достаточно руководствоваться формальным алгоритмом.

Date: 2015-07-23; view: 1099; Нарушение авторских прав